There is an urban legend often told by people who deal with data mining which says that an association rule learning algorithm was used by retail stores in the 90s to check the associations between the products their customers buy. According to the story, they discovered that customers who buy diapers also tend to buy beer.

Table of Contents

Apriori
Why is this algorithm so powerful?

We are not sure whether the story is true and there used to be a long discussion about it, for example, D. J. Power wrote a long section about it in his newsletter in November 2002.

Association rules were introduced for discovering regularities between products in transaction data in supermarkets. In general, we can detect that if a person buys beer, the same person is more likely to buy also burgers (or diapers).

To identify the association rules, we must make three calculations. The first one calculates how often the product is purchased. The result is called “support” and the equation is quite straightforward.

After that, we start grouping the products. Now, we can calculate “confidence.” Confidence tells us what proportion of transactions which consist of product A, also contain product B.

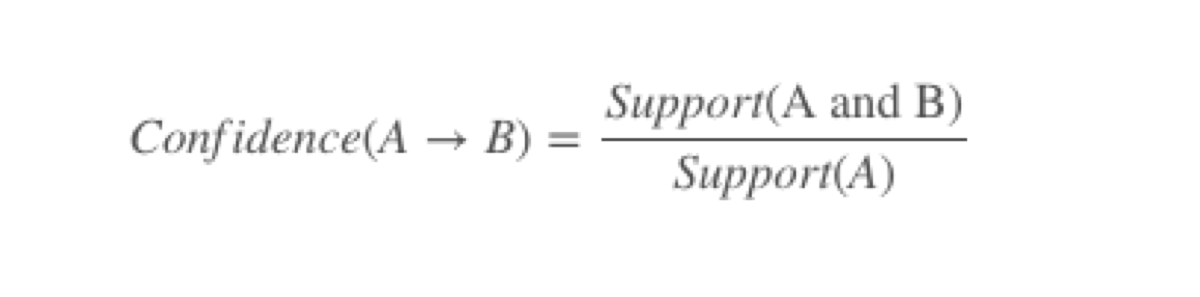
As the last step, we calculate the “lift’. It is the value that tells us how likely item B is bought together with item A. Values greater than one indicate that the items are likely to be purchased together.

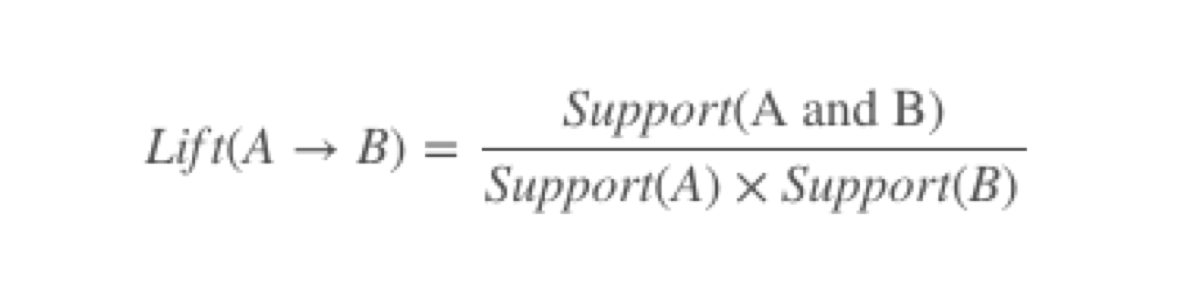
In practice, we are not interested in pairs of items, but the whole sets. It means that we are going to end up with a cartesian product of items in the shop and then we generate a cartesian product of the product pairs and the products again! And again!

Apriori

Calculating the lift of all such combinations will take some time.

The solution to that problem is a crucial part of the Apriori algorithm. In this method, we define the minimal support of an item. Then we skip the things which support is below the threshold.

That is done at every step. We do it when we have only one item in the set, when we add a second item to it and when we have even more items. At every step, we skip the sets which don’t occur often enough.

Such approach allows us to focus on associations that occur between products that are purchased often. After all, who cares about something that clients buy once a year?

Why is this algorithm so powerful?

Its power is based on its simplicity. We need to make only three calculations, and we get something that works reasonably well in both retail and online recommendations.

After all, we can always replace “buying a product” with “liking a movie” and get similar associations in an entirely different context, then we can match the user’s likes to any of those associations and give the user a list of movies that are often watched by similar users.

It won’t beat Netflix or YouTube recommendation algorithms, but it is just a few lines of code and only basic mathematical operations.

That is why I like it. I appreciate the elegance and simplicity of that algorithm. In the industry overhyped with deep learning, it is nice to read about something which requires only elementary school math. Even if we never use it again, it is good to know a method that was an important part of data science history.

Apriori algorithm explained

Apriori

Why is this algorithm so powerful?

How to change plot size in Jupyter Notebook

How to display mathematical equations in Jupyter Notebook

Apriori algorithm explained

Apriori

Why is this algorithm so powerful?

How to change plot size in Jupyter Notebook

How to display mathematical equations in Jupyter Notebook

Related Posts

I worked as a data scientist and that was the worst job I have ever had.

How to remove outliers from Seaborn boxplot charts

Pandas stack and unstack explained