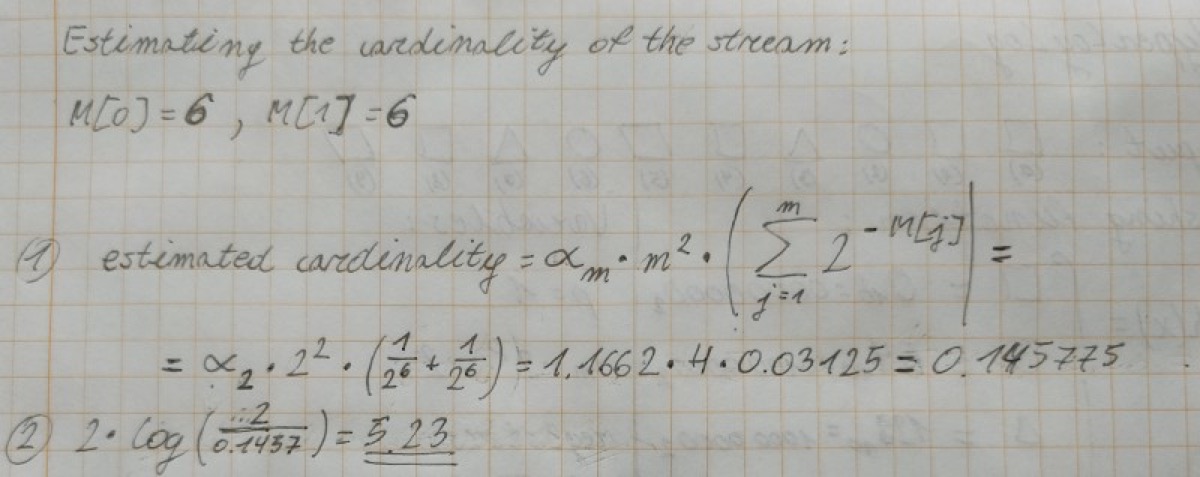I have a task for you. I send you an infinite stream of objects, and your job is to give me the number of unique elements you have seen so far. I may send you 10 elements and then ask you how many have you seen or wait until you receive 1 million elements.
Table of Contents
There is at least one huge problem. You can add elements to a set, and when I ask you about the number of unique elements, you can give me the size of the set. Such a solution works perfectly in case of 10 elements. It may work correctly even in the case of 1 million elements, as long as you can store them somewhere.
The stream is infinite. At some point, you are going to run out of memory. Don’t be scared. I have one good news for you ;) I don’t need an exact number of unique elements, an approximation is enough for me.
You don’t need hundreds of terabytes of memory. You can accomplish that using just a few kilobytes. Hype-driven, big data developers are going to hate it ;)
Cardinality estimation algorithm
Task
I have a stream of squares, triangles, circles, and parallelograms. I want to count the cardinality of that stream. Obviously, the exact cardinality is equal to 4. I want to explain the concept, so don’t expect the correct result. This algorithm works well with a massive number of unique elements.
What we need?
-
HyperLogLog algorithm — probabilistic counting algorithm that estimates the number of unique elements in the given dataset
-
a hashing function that accepts a shape as a parameter and returns an unsigned byte. Note that the hash values must be uniformly distributed.
-
parameter m, in this case, m = 2, the number of registers
-
parameters p = 1, because m = 2^p
-
two bytes of memory to store the registers used by HyperLogLog, at the beginning both registres store 0.
-
the bias parameter — explained at the end of this article
Steps
-
Pass the object to the hashing function and get a hash number.
-
Convert the number to its binary representation.
-
Take the first p bite (in our example, the first bite). Use it as the identifier of the registry.
-
Pick the correct registry.
-
Take the other seven bites of the hash number, let’s call them x.
-
Calculate the number of leading zeros in the binary representation of x+1
-
Compare the number of leading zeros with the current value of the selected registry, pick the larger number.
-
Store the number calculated in step 7 as the new value of the registry.
To estimate the number of elements use the following equation:
![alpha_m =the bias parameter, m = number of registers, M = an array of registers so M[j] means the j-th registry](/images/2018-08-19-count-unique-elements-of-an-infinite-stream-of-objects/number_of_elements.png)
We can calculate the bias parameter using this equation:
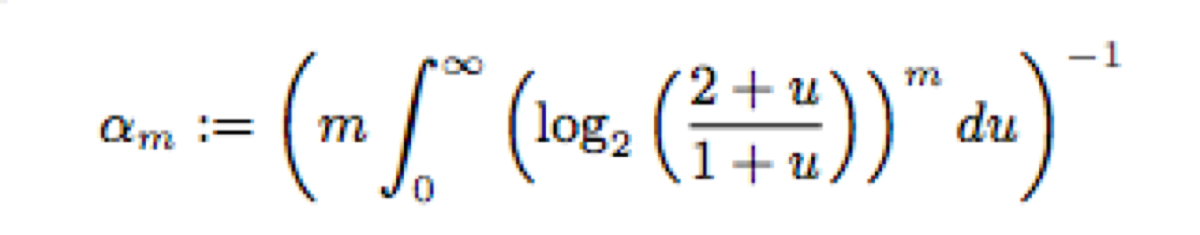
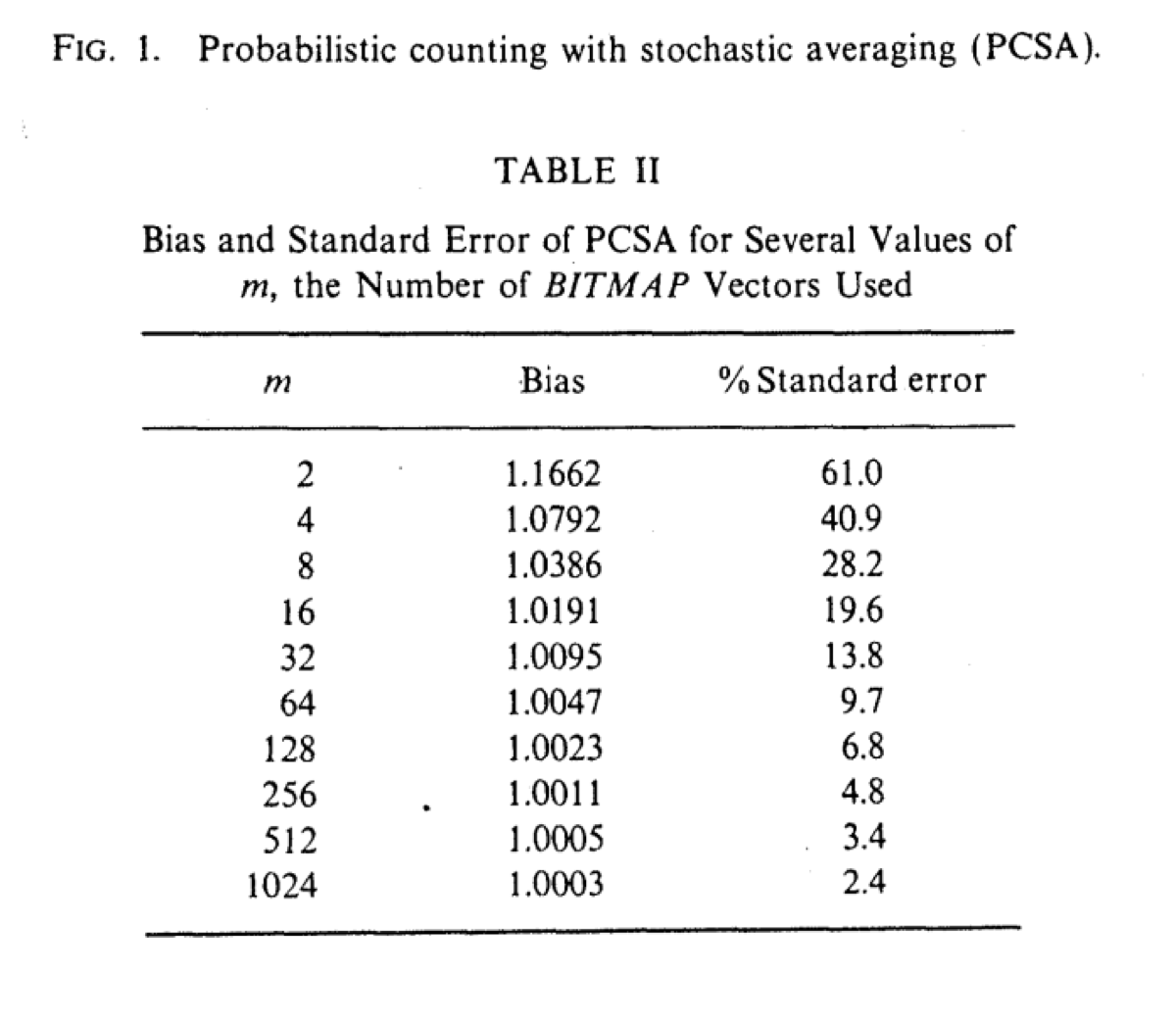
or use the table of values from the “Probabilistic Counting Algorithms for Data Base Applications” paper by Philippe Flajolet:
In 2013, a few improvements of the algorithm have been proposed by Stefan Heule, Marc Nunkesser, and Alexander Hall in their paper: “HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm.” For example, if the number of elements is small, multiply it a little bit: m * log(m / estimated cardinality)
That is the part we need ;)
Let’s do it with pen and paper

Now we can estimate the cardinality of the stream of shapes: