In this blog post, I am going to describe three encoding methods that turn categorical variables into numeric features and show their implementation in Scikit-learn and Pandas.
Table of Contents
Imagine that we have a categorical variable which describes the types of coffee available at a tiny cafe. There are only three distinct values: Americano, espresso, and latte macchiato. I want to use a logistic regression model, so I need numeric variables. Let’s look at the methods of encoding them.
One-hot encoding
In one hot encoding, we turn the categorical variables into boolean variables. The variable answers the question: “Is it X?” In my case, I am going to have three features: “Americano,” “espresso,” and “latte macchiato.” Hence, the variable answers questions like “Is it Americano?”
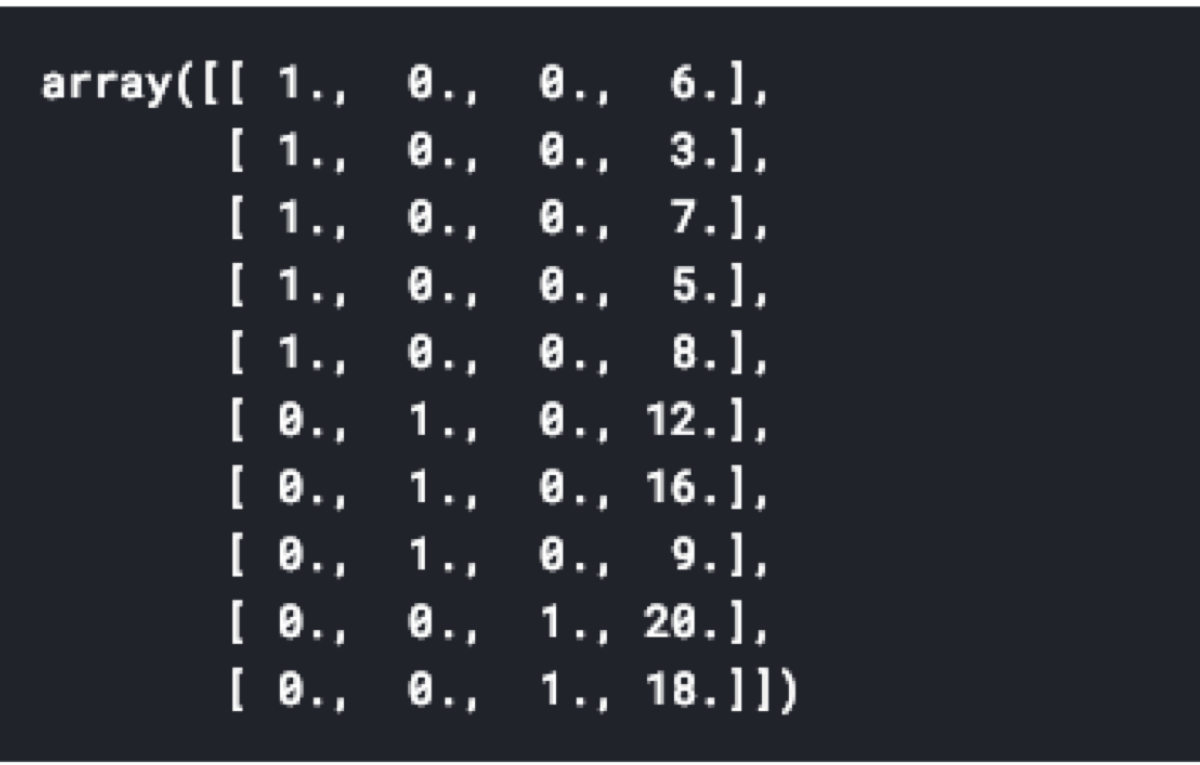
This is how we can use one-hot encoding in scikit-learn:
import pandas as pd
data = pd.DataFrame([
['americano', 6],
['americano', 3],
['americano', 7],
['americano', 5],
['americano', 8],
['espresso', 12],
['espresso', 16],
['espresso', 9],
['latte', 20],
['latte', 18]
],
columns=['coffee', 'time_spent_in_min']
)
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
categorical_features = ['coffee']
categorical_transformer = Pipeline(steps=[
('onehot', OneHotEncoder())])
preprocessor = ColumnTransformer(
remainder = 'passthrough',
transformers=[
('categorical', categorical_transformer, categorical_features)
])
preprocessor.fit_transform(data)
There is one huge problem with one-hot encoding. The features are linearly dependent. Linear dependence means that if you tell me what is the value of “Is it Americano?” and “Is it espresso?”, I can tell you whether it is a latte macchiato or not. Which means that there is no reason to have the “Is it latte macchiato?” variable because the model can infer it from other features.
Obviously, we can decide to use the all-zeros variable to denote missing value. In this case, the model can return some “default” value, like the mean of the target variable. If we decide to encode missing values in such a way, we can ignore the linear dependency issue.
Want to build AI systems that actually work?
Download my expert-crafted GenAI Transformation Guide for Data Teams and discover how to properly measure AI performance, set up guardrails, and continuously improve your AI solutions like the pros.
Dummy coding
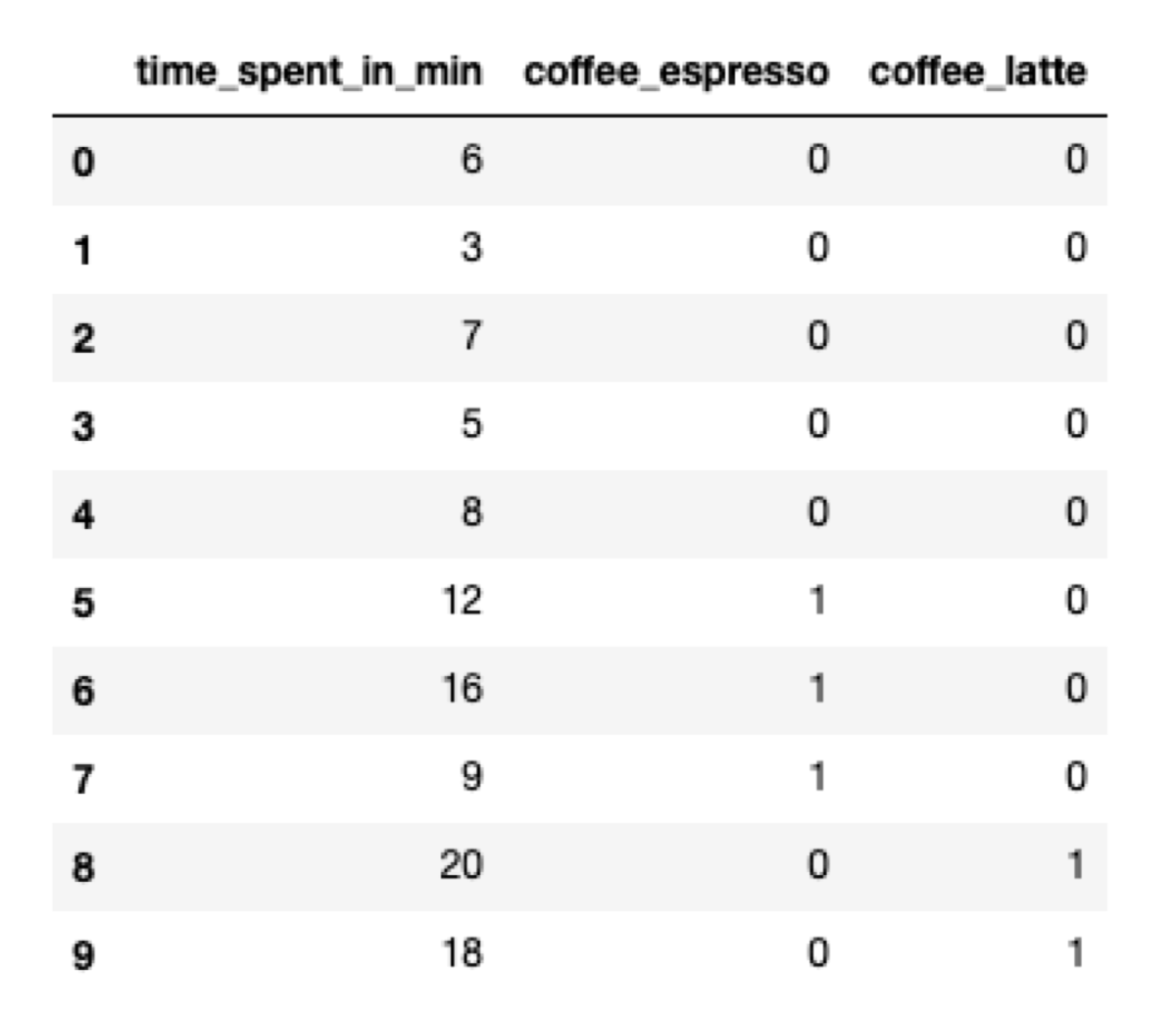
Dummy coding solves the linear dependence problem. The only difference between this encoding method and one-hot encoding is the lack of one feature column.
categorical_features = ['coffee']
pd.get_dummies(data, columns = categorical_features, drop_first = True)
Besides having the advantage of smaller feature space, this encoding gives us also the ability to interpret linear models easier. If I want to predict how much time a customer is going to spend in the restaurant and I know the type of coffee they ordered, I am going to end up with a linear model which looks like this:
time spent = is_it_americano * difference_between_avg_time_spent_by_americano_drinkers_and_latte_drinkers +
differenis_it_espresso * difference_between_avg_time_spent_by_espresso_drinkers_and_latte_drinkers +
avg_time_spent_by_latte_macchiato_drinkers
That may be difficult to explain because the coefficients represent the value which is relative to the reference category (in this case the latte drinkers).
In the case of one-hot encoding, such explanation is much easier because the intercept term would denote the average time spent by all customers. The coefficient would represent the difference between the average time spent by all customers and the drinkers of a particular coffee.
Effect coding
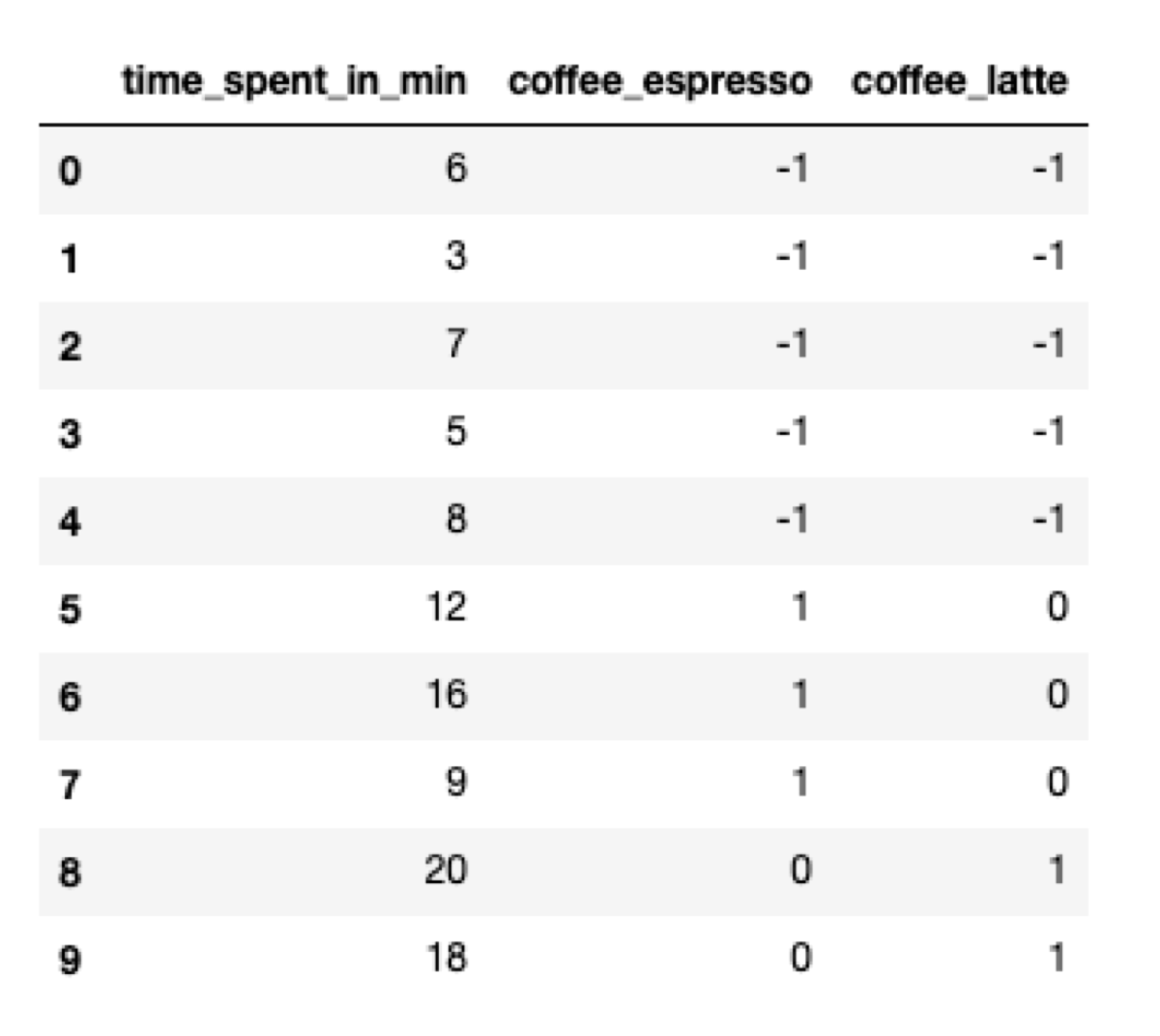
Effect coding emphasizes encoding the difference between categories even more. This time we must choose one category to be the reference category. Let’s choose Americano as the reference category. We are going to encode it as a vector of all -1s. The other categories are encoded like in the dummy coding.
The intercept term is equal to the average time spent by all customers. The features denote the difference between the global average and the average of the categories.
import numpy as np
categorical_features = ['coffee']
encoded = pd.get_dummies(data, columns = categorical_features, drop_first = True, dtype = np.int8)
# the dtype is important because the default is np.uint8 - *unsigned* 8-bit integer
encoded.iloc[0:5:,1:3] = -1
