If you want to move from just fighting the symptoms of hallucinations to building systems that prevent them, you need greater control over the LLM’s output. That starts with understanding the sampling methods used by the models.
Table of Contents
- Why do we need sampling?
- Sampling methods
- Top-k sampling
- Probability adjustment
- Logits bias
- Combining adjustments with sampling methods
- Controlling hallucinations with sampling, temperature, and logits bias
- Summary
- References
Why do we need sampling?
Sampling is needed in generative AI to introduce controlled randomness and diversity into the outputs rather than always selecting the most likely next token. Without sampling, a language model would always choose the highest probability token at each step, leading to repetitive, predictable, and potentially uninteresting text.
When an LLM generates the output, the LLM uses the probability distribution of the next token to choose the most likely token. The probability distribution is calculated based on the model’s weights and the input tokens. Only one token is produced at a time. Therefore, to generate a longer text, we need to use the model in a loop while adding the previously generated token to the input.
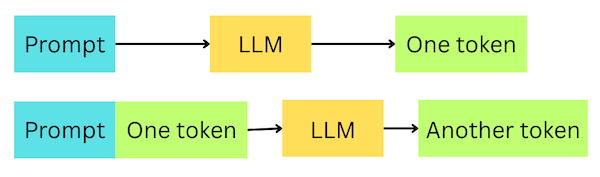
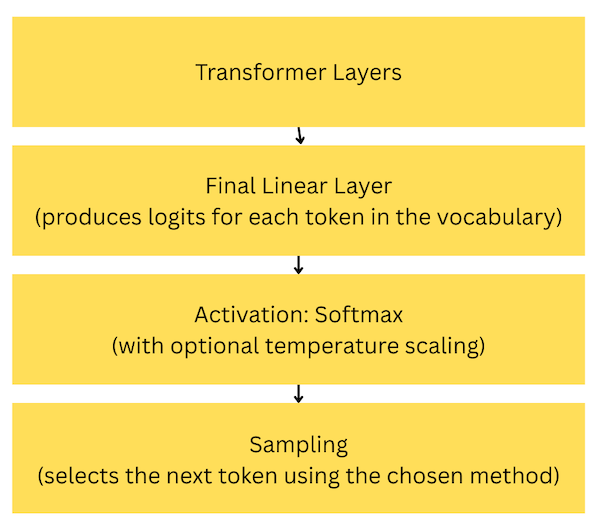
Because a fully deterministic model isn’t always desirable, the token selection process (sampling) consists of several steps:
- First, the data runs through the transformer layers.
- Then, the data reaches the final (linear) layer, where a value is assigned to every possible token in the model’s vocabulary. We call those values logits.
- The logits are then passed through a softmax function to convert them into probabilities. The softmax function may use the temperature parameter to increase the likelihood of already high-probability tokens or flatten the distribution (to make the model more random).
- The probabilities are then used to sample the next token. Below, I describe several sampling methods.
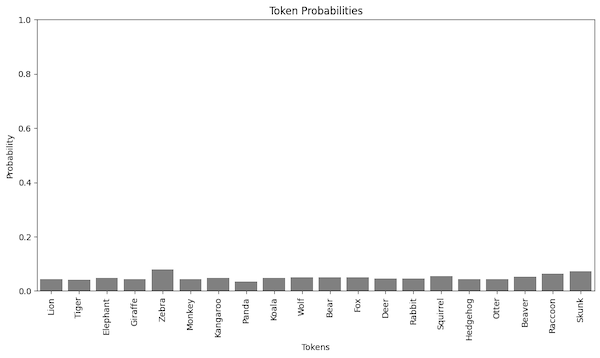
Sampling methods
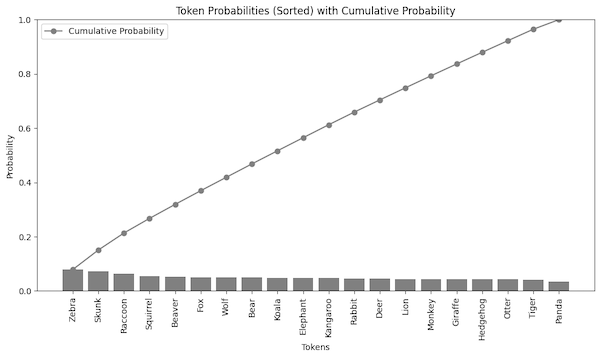
Before we talk about sampling methods, we need the data. Let’s say our model generates only a single token, and the token is one of the 20 possible animal names. I have generated the probabilities of such tokens randomly. The values are in the range of 0-1, and they sum up to 1. In a real model, those values would be the output of the softmax function with temperature set to 1.
Greedy sampling
Greedy sampling is the simplest sampling method. The method selects the most likely token at each output generation step. Fully deterministic. Fully boring. We can get the deterministic behavior by setting the temperature to 0, though temperature 0 isn’t always truly deterministic.
Top-k sampling
The top-k sampling is still relatively simple. We order the probabilities from the highest to the lowest and select the top-k tokens.
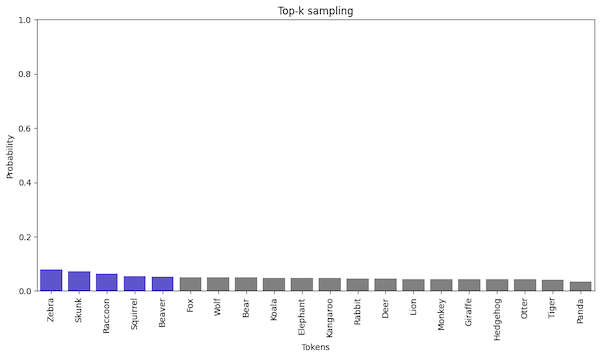
After selecting the top-k tokens, we normalize the probabilities to sum up to 1. We can normalize the probabilities in two ways:
- by dividing the probabilities by the sum of the top-k probabilities, which gives us a probability distribution proportional to the original probabilities of the top-k tokens
- by using a uniform distribution which turns sampling into a random selection from the top-k tokens
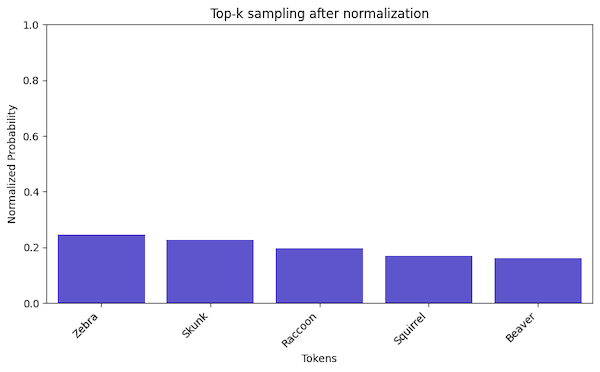
Regardless of the normalization method, the next token is selected based on the probabilities we produce during normalization.
Top-p sampling (nucleus sampling)
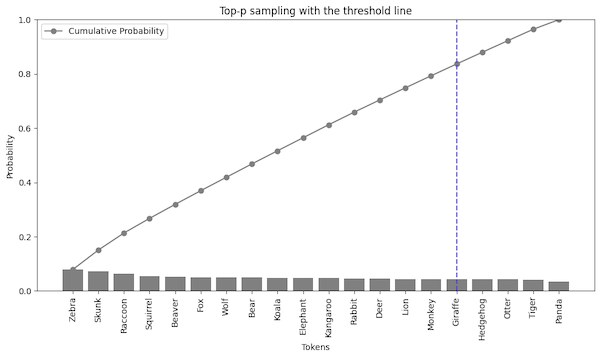
Instead of deciding how many tokens to select, we can choose how much probability mass (cumulative probability) to select. We start with the highest probability token and keep adding tokens to the selection until we reach the desired probability mass.
For example, we can consider only tokens that add up to 0.8 of the probability mass. Then, we take all of the tokens before the threshold.
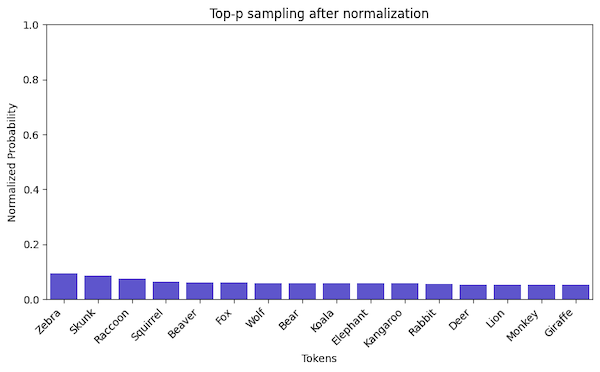
And normalize the probabilities of the selected tokens. (Again, we have two ways. In the image, I used proportional normalization.)
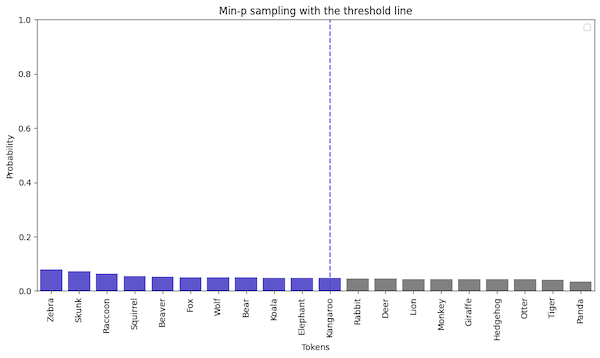
Min-p sampling
Min-p sampling reverses the logic. Instead of selecting the most probable tokens, we drop the tokens below the threshold. We allow more randomness in the output while preventing irrelevant tokens from being selected.
The Min-p sampling process has three steps:
- First, we set the min-p threshold. Because there is no way to know if we get any tokens above this threshold, the threshold is scaled by the value of the most probable token. So the final threshold is:
user_selected_min_p * probability_of_the_most_probable_token. - Tokens above the threshold are selected.
- The probabilities of the selected tokens are normalized.

Probability adjustment
In addition to the sampling methods, we can adjust the tokens’ probabilities by using the temperature parameter or adding bias to the logits. The adjustment happens before or inside the softmax function so that we can combine adjustments with sampling methods. (Even though, OpenAI doesn’t recommend it.)
Temperature
Temperature controls the “sharpness” of the probability distribution. The higher the temperature, the more random the output. The lower the temperature, the more deterministic the output. We say it’s sharpness because when you look at the probability distribution, the lower the temperature, the more concentrated the probability mass is around the most probable token (a sharp peak in the distribution chart). On the other hand, the higher the temperature, the more spread out the probability mass is, and the probability distribution looks more like a uniform distribution.
The formula for the softmax function with temperature adjustment is:
def scaled_softmax(logits, temperature=1.0):
scaled_logits = logits/temperature
return np.exp(scaled_logits) / np.sum(np.exp(scaled_logits), axis=-1, keepdims=True)
As we see, temperature zero leads to an undefined value. Some open-source models (like Llama) don’t allow the temperature to be zero. In others (for example, OpenAI API), setting the temperature to zero switches to greedy sampling (always selecting the most probable token) instead of adjusting the probabilities.
Let’s start with the temperature set to 1.0. We see the same probabilities as in the first image.

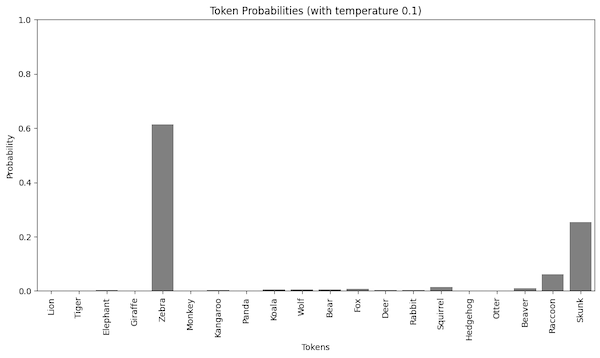
Now, we set the temperature to 0.1. We see the probabilities of already probable tokens are increased while the probabilities of the less probable tokens are flattened out almost to zero. As a consequence, a low temperature makes the model more deterministic.
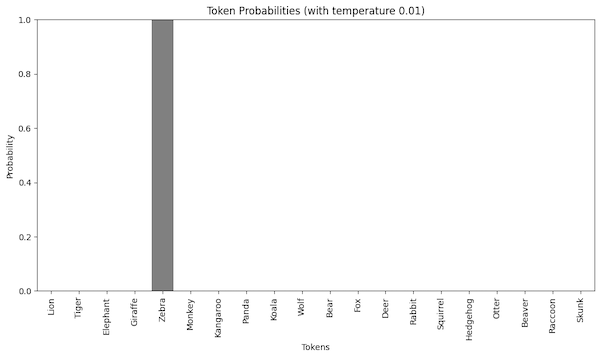
If we decrease the temperature even more, we will make one token dominate the output.
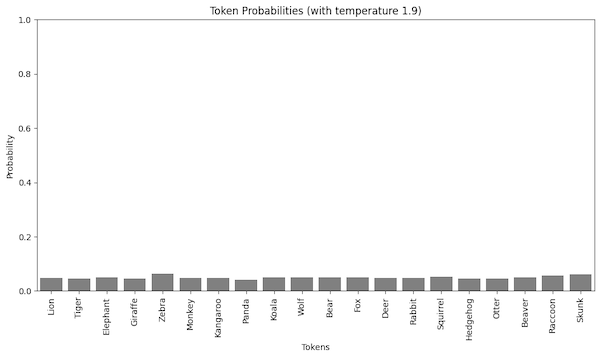
If we want a more random output, we can set the temperature to a higher value. For example, when I set the parameter to 1.9, the logits we used before are scaled to almost a uniform distribution.
Logits bias
Instead of using mathematical functions to adjust the probabilities, we can also add a bias to the logits. The bias is added to the logits before the softmax function. It’s a way to control the probabilities of the tokens manually. We can use logits bias when we don’t want specific tokens to ever occur in the output or when we want to favor certain tokens. Of course, we can combine the bias with the temperature adjustment and sampling methods.
Let’s say we want to favor the wolf token and disfavor the zebra token while removing the skunk token from the output. We can achieve such a behavior by adding a bias to the logits.
bias = {"Wolf": 2, "Skunk": -100, "Zebra": -2}
biased_logits = np.copy(logits)
for token, bias_value in bias.items():
if token in tokens:
token_index = tokens.index(token)
biased_logits[token_index] += bias_value
probabilities = scaled_softmax(biased_logits, temperature=1.0)
Even with the temperature set to 1.0, the probabilities look entirely different. The wolf token is now the most probable one.
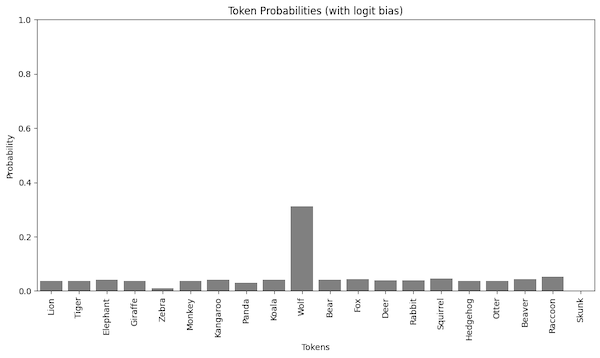
Combining adjustments with sampling methods
We can combine all three operations (sampling, temperature adjustment, and logits bias) because they happen independently in a constant order.
- First, logits are calculated so we can add bias to them.
- Then, the probabilities are calculated using the softmax function. We can use the temperature parameter to adjust the probabilities.
- Finally, we can select the next token using the sampling method.
However, modifying everything at once makes it hard to understand the impact of each adjustment. The OpenAI documentation suggests using either temperature or top-p parameter, but not both.
Also, we must remember that the logits bias applies to tokens, not words. A word can be composed of multiple tokens or occur multiple times in the vocabulary (for example, with and without the preceding space character).
When we run an open-source model locally, we can modify those parameters for every token. Third-party models allow us to set those parameters once and apply them to all tokens generated in a single request. Finally, not every API supports all sampling methods or adjustments. For example, OpenAI gives us only temperature, top-p, and logits bias.
Controlling hallucinations with sampling, temperature, and logits bias
Neither of those parameters will be enough to control hallucinations, but they certainly can help. In the Microsoft Codex documentation, they recommend setting the temperature to 0.1 or 0.2 when we use the model to generate code. Similarly, we can use low-temperature settings in RAG applications while generating queries (often SQL, so code) or in the agentic applications while generating tool call parameters.
Setting the API temperature to 0, or close to zero (such as 0.1 or 0.2) tends to give better results in most cases. Unlike GPT-3 models, where a higher temperature can provide useful creative and random results, higher temperatures with Codex models might produce random or erratic responses.
When we want more creative and diverse output, the Turning Up the Heat: Min-p Sampling for Creative and Coherent LLM Outputs paper recommends using min-p sampling. Of course, for now, only open-source libraries support min-p sampling.
Zep’s guide to Reducing LLM Hallucinations suggests lowering the temperature and the top-p parameter to reduce the tokens to only top predictions, which, according to the authors, are more likely to be correct. The reasoning looks as if it made sense, but does it? What if the top prediction is wrong because we retrieved the wrong document and put the document in the model’s context? That’s why I said those parameters can help, but they are never enough. For a comprehensive approach to measuring and fixing hallucinations, you need architectural solutions, not just parameter tuning. They are tools in the toolbox, but you need an architectural blueprint to truly solve the AI hallucination problem.
Summary
| Method | Determinism Level | Use Case | Best For |
|---|---|---|---|
| Temperature | Adjustable (0.0-2.0) | General text generation | Controlling randomness vs determinism |
| Top-p (nucleus) | Semi-deterministic | Creative writing | Maintaining coherence while allowing diversity |
| Top-k | Semi-deterministic | Code generation | Limiting vocabulary to most likely tokens |
| Min-p | Creative | Creative tasks | Generating diverse yet coherent outputs |
| Logits bias | Highly controlled | Specific token control | Forcing or preventing specific token selection |
| Greedy decoding | Fully deterministic | Code, factual responses | When reproducibility is critical |

