What size is going the output have after applying a convolutional pooling layer? I used to have no idea. I sort of could imagine what happens when a filter is applied, but when we added padding and increase the stride, my imagination got lost.
Table of Contents
If you have a similar problem, this article is for you. I am going to explain how the filter size influences the size of the next layer, how to use padding, and what happens when you use stride.
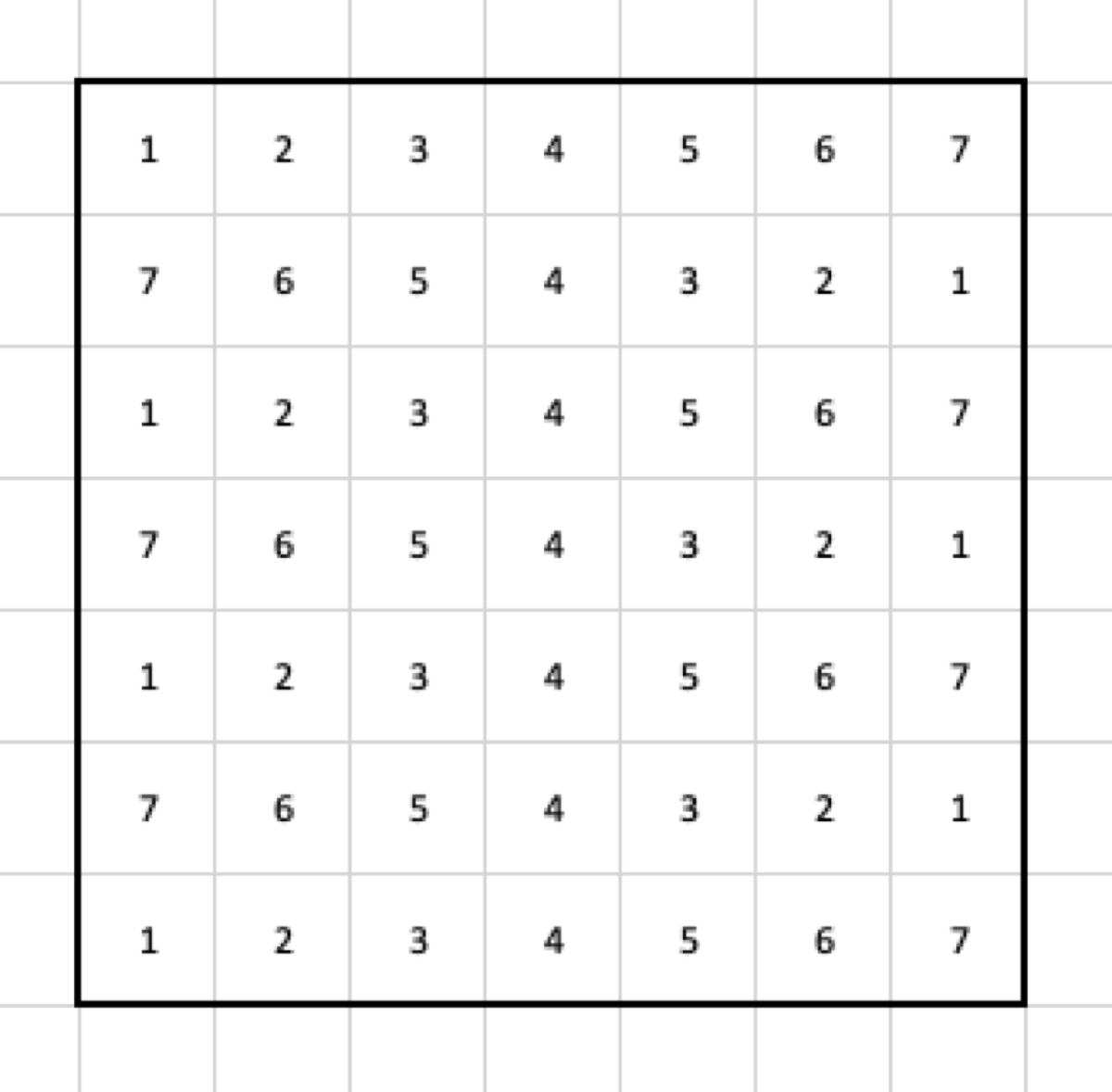
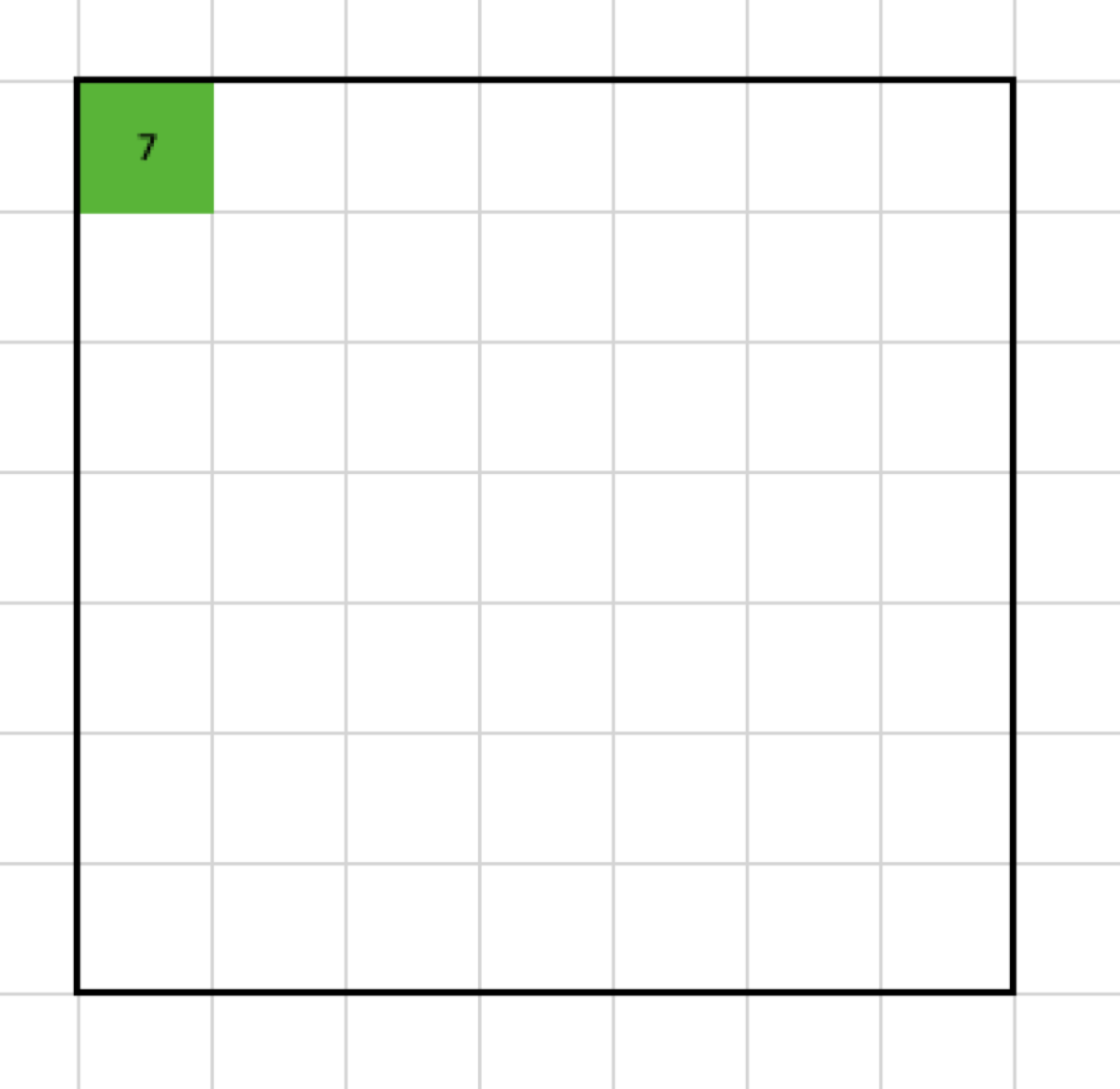
Input
For the sake of an example, let’s use the following data as the input for the pooling layer. Also, I am going to use the max pooling, just because it is simple and makes a good example.
Filter
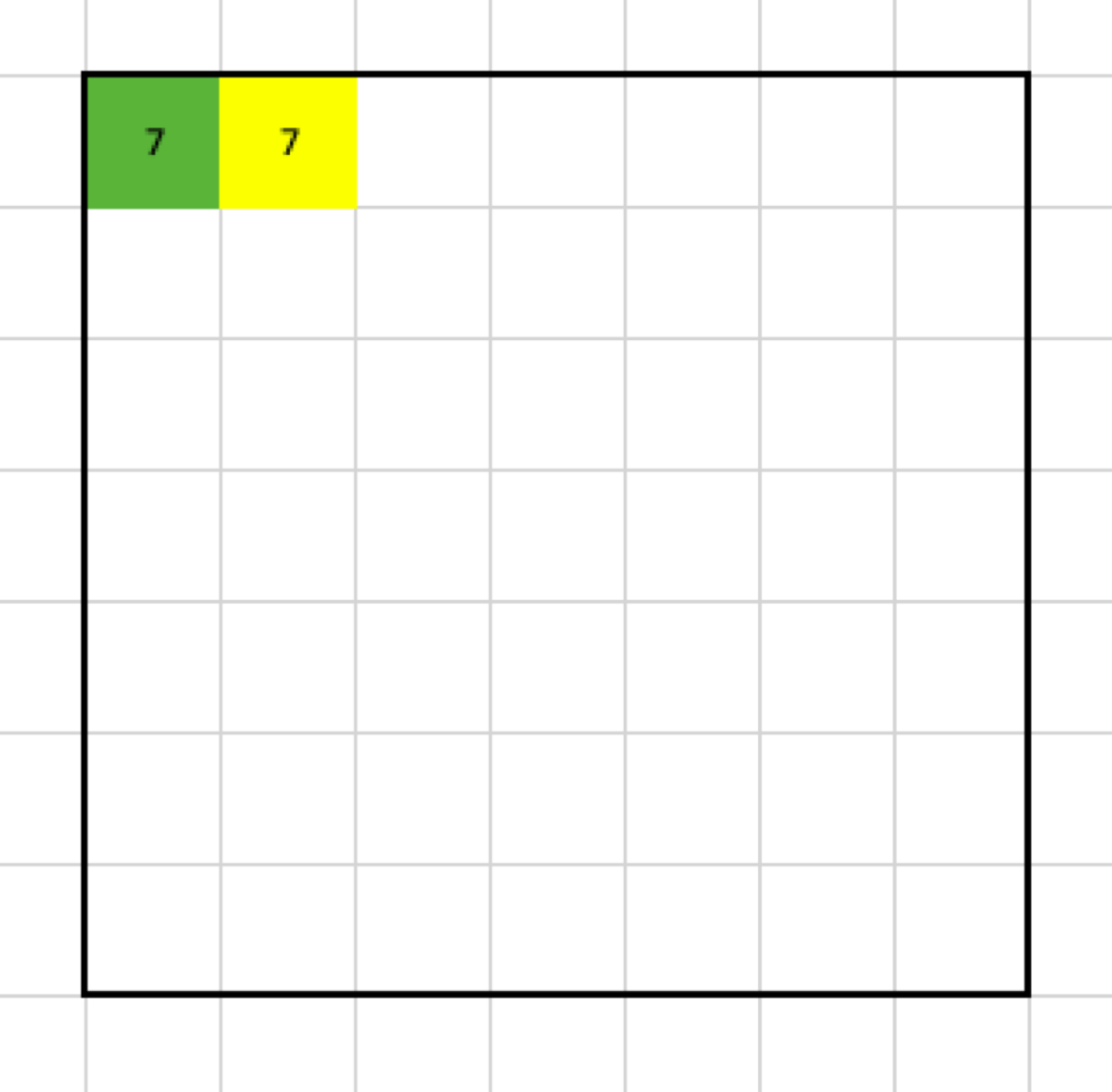
I decided to use a 3x3 filter. It means that the output shrinks by two columns and rows. Why? Let’s look at the result of applying the max pooling to the first set of cells.
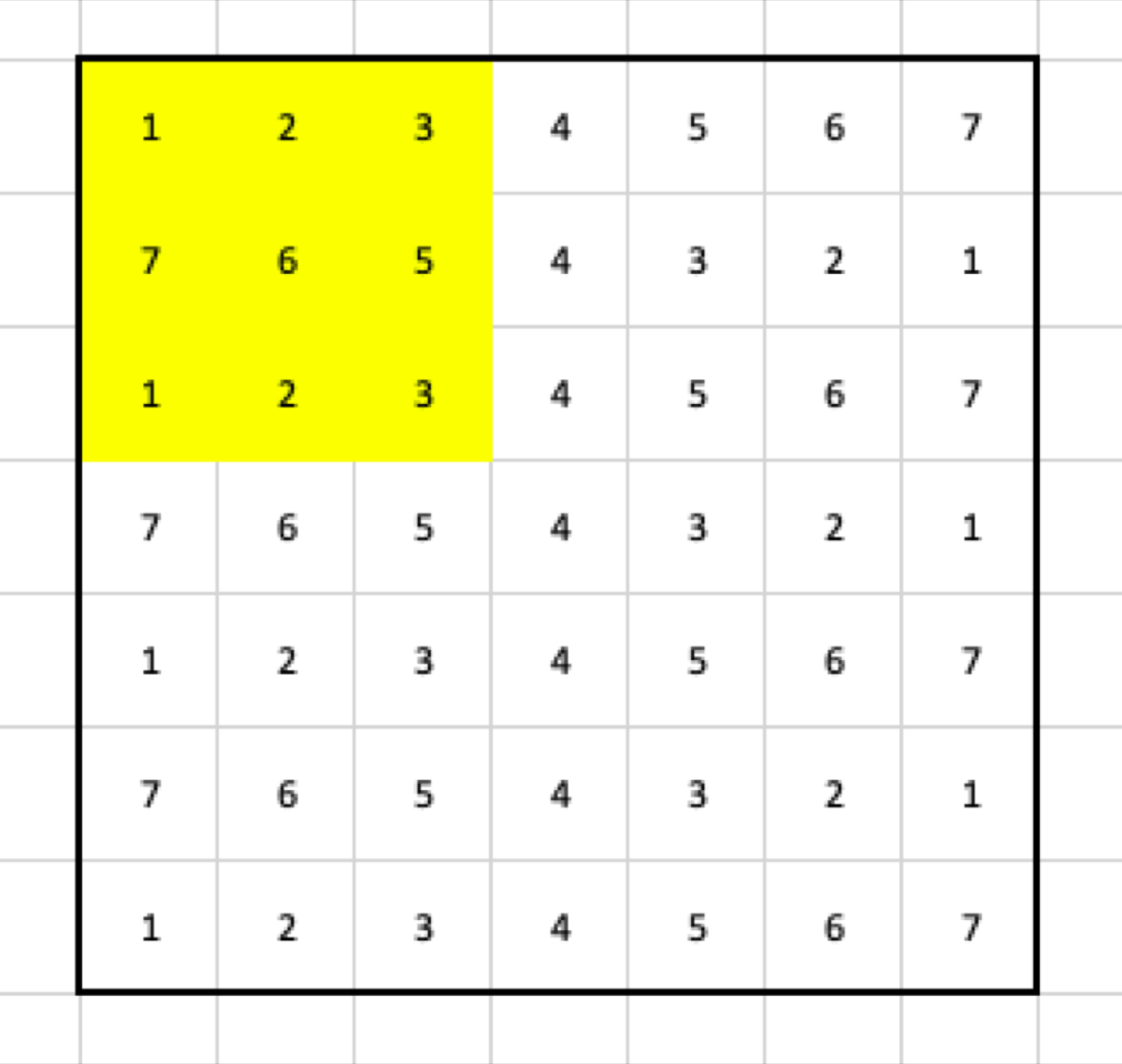
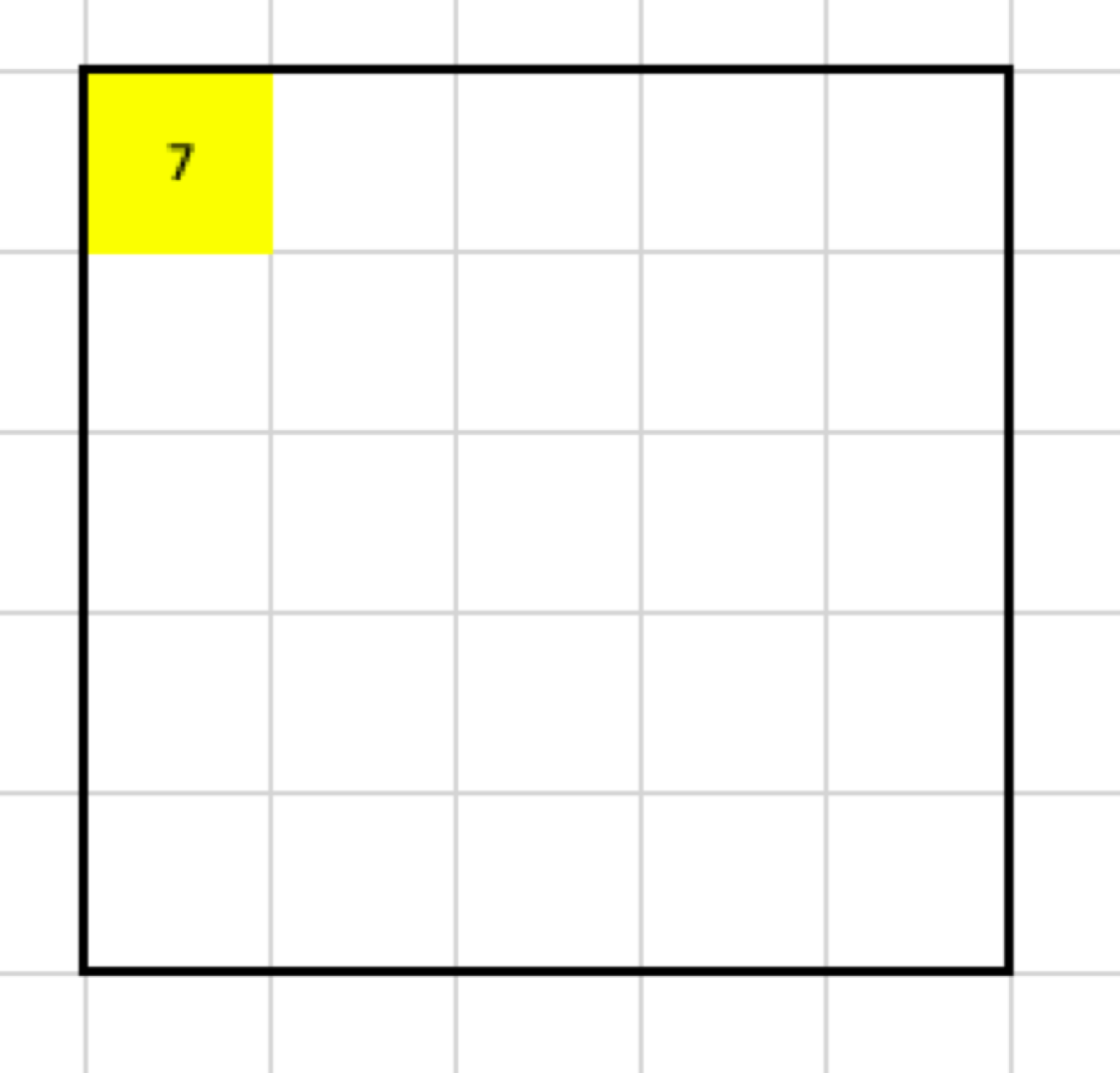
The maximal value of the selected cells is 7, so the output looks like this:
Now, I have to move my filter. To make things easy, in the first example, the stride has to be 1, so let’s move the filter by one column.
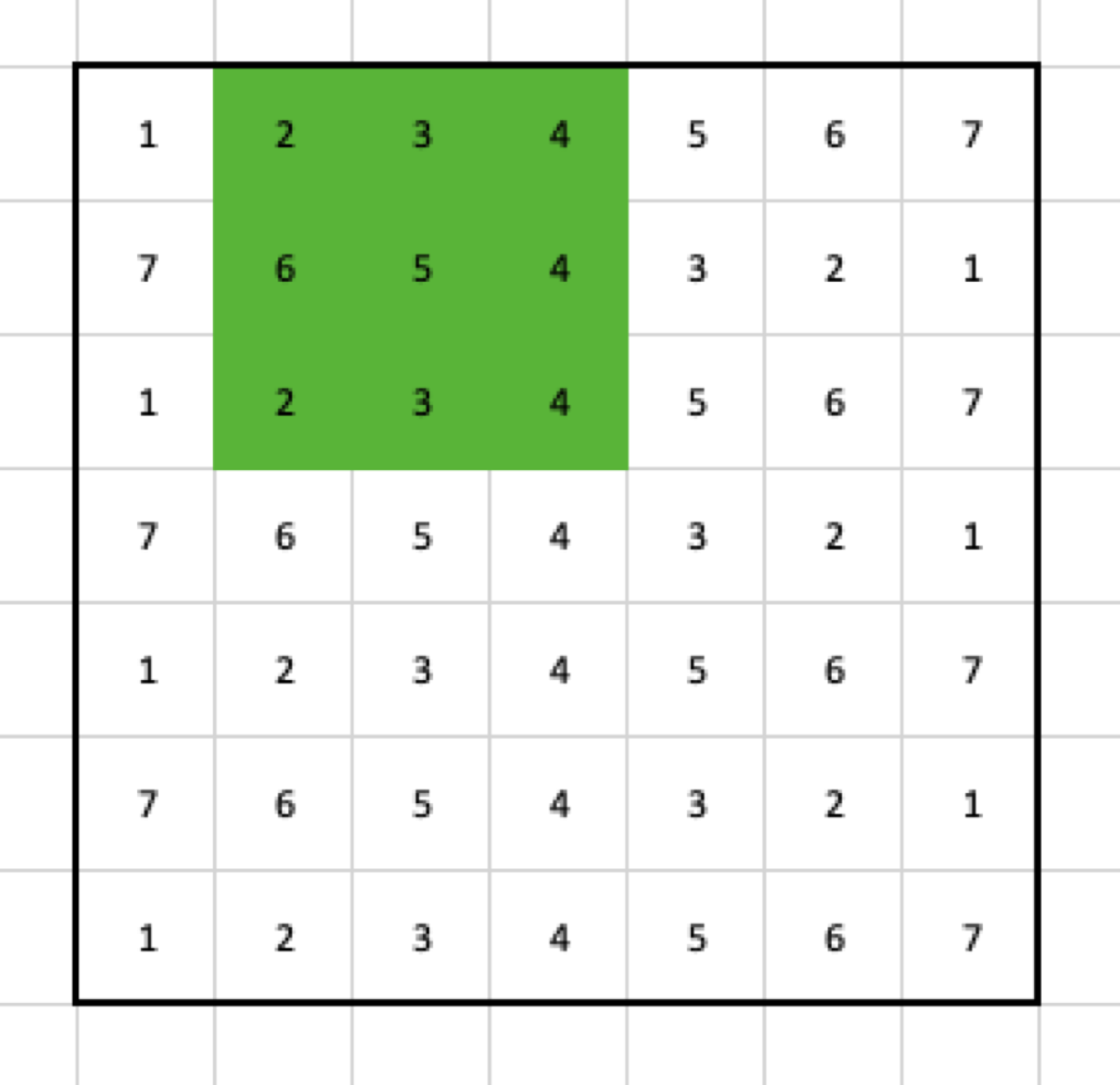
That gives me another value for the output:
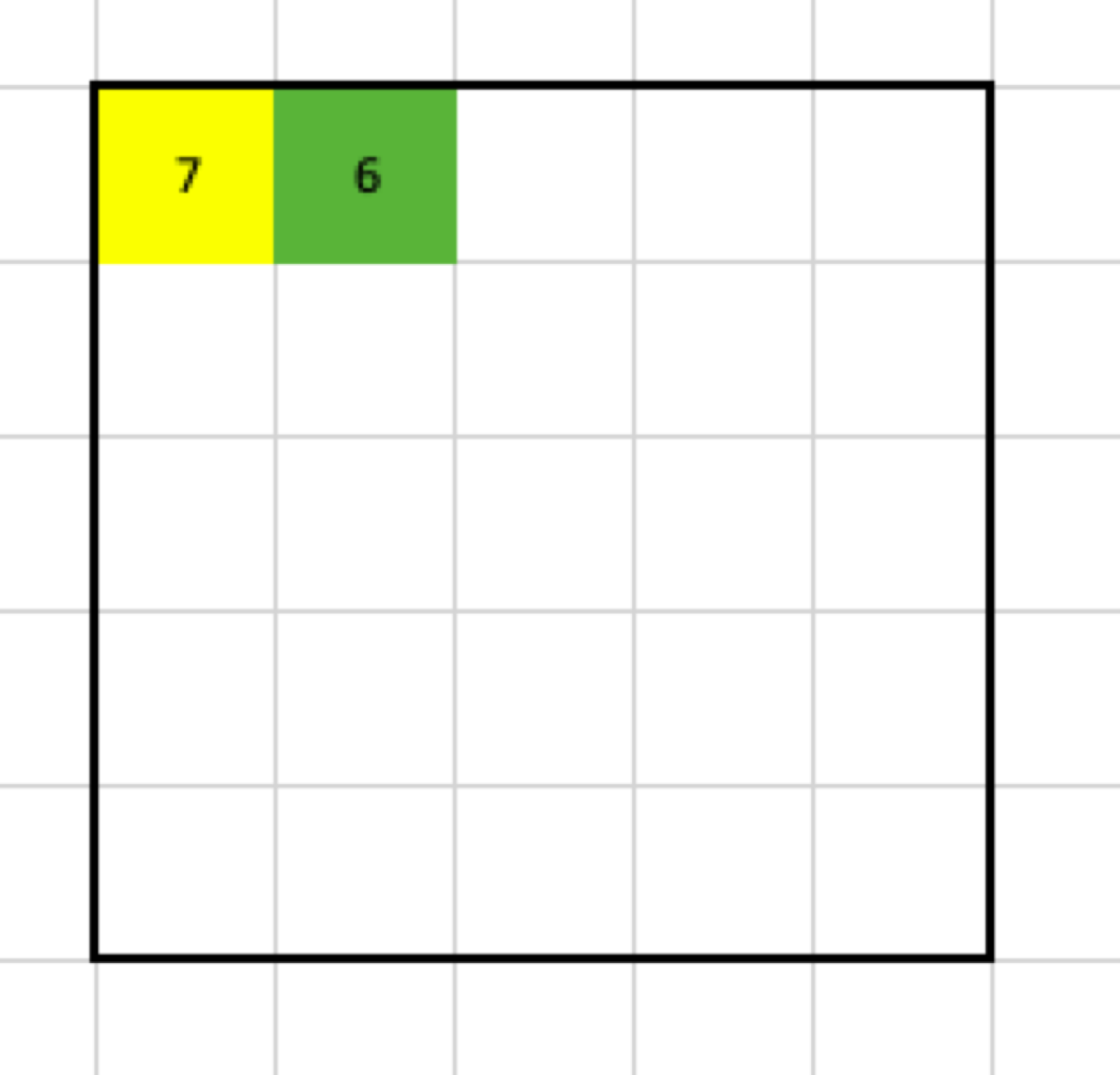
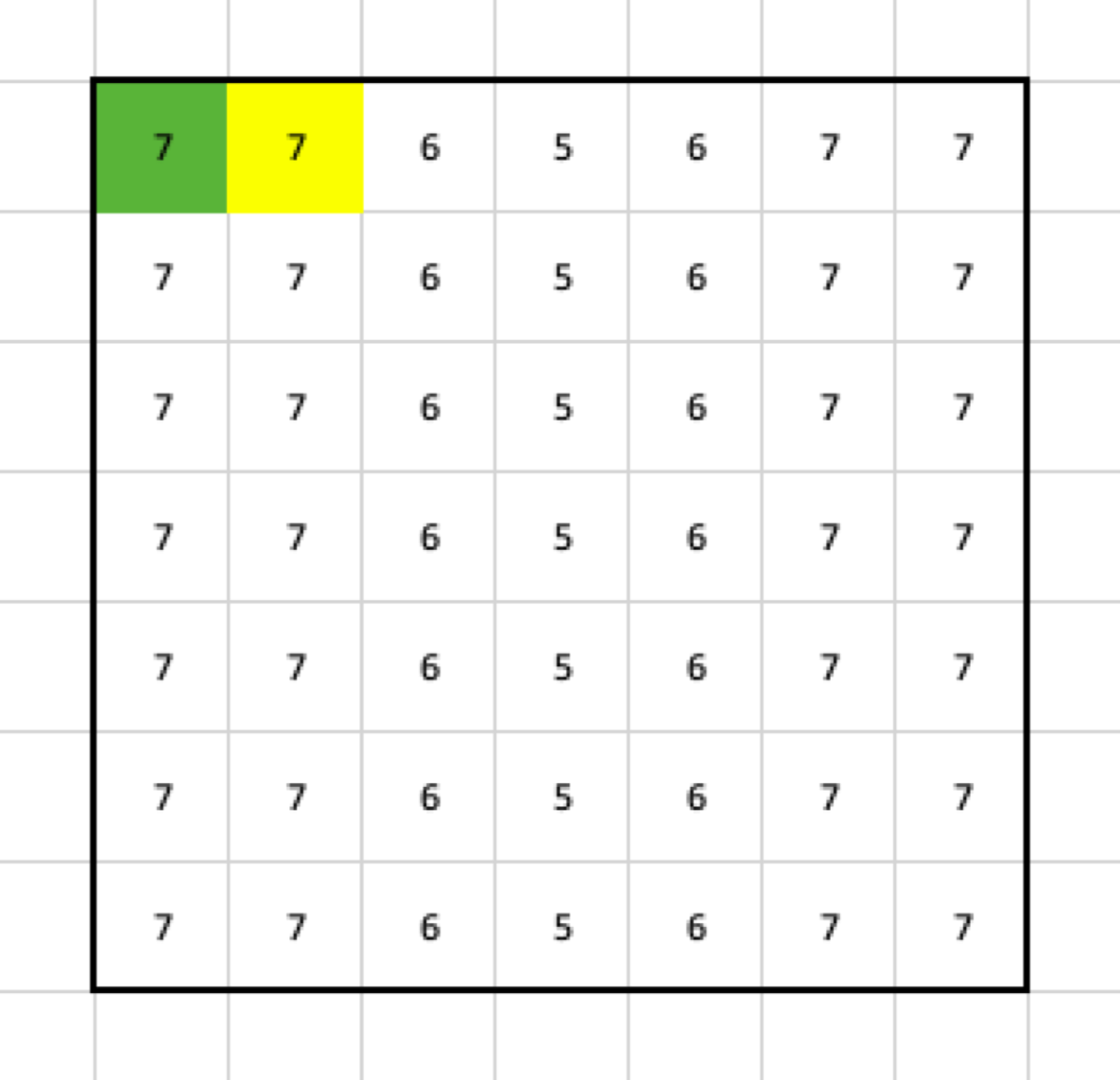
If I continue applying the max pooling filter, I am going to end up with this result:
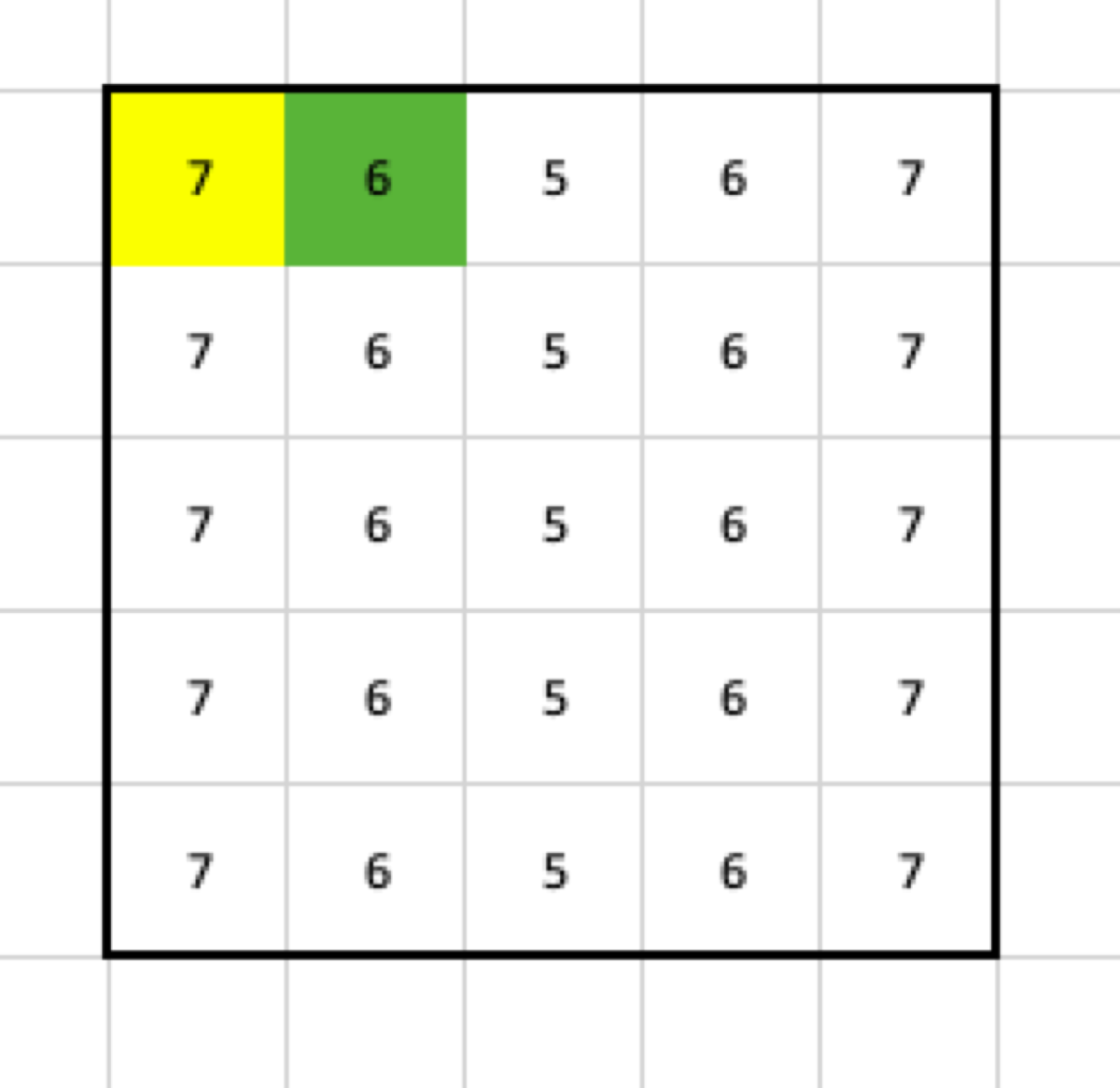
What happened? From the pooling filter, I get only one value, so when the stride is 1, and there is no padding, the output is going to shrink by:
number_of_lost_columns_or_rows = the_size_of_the_filter - 1
(in this example, 2 columns and 2 rows)
Padding
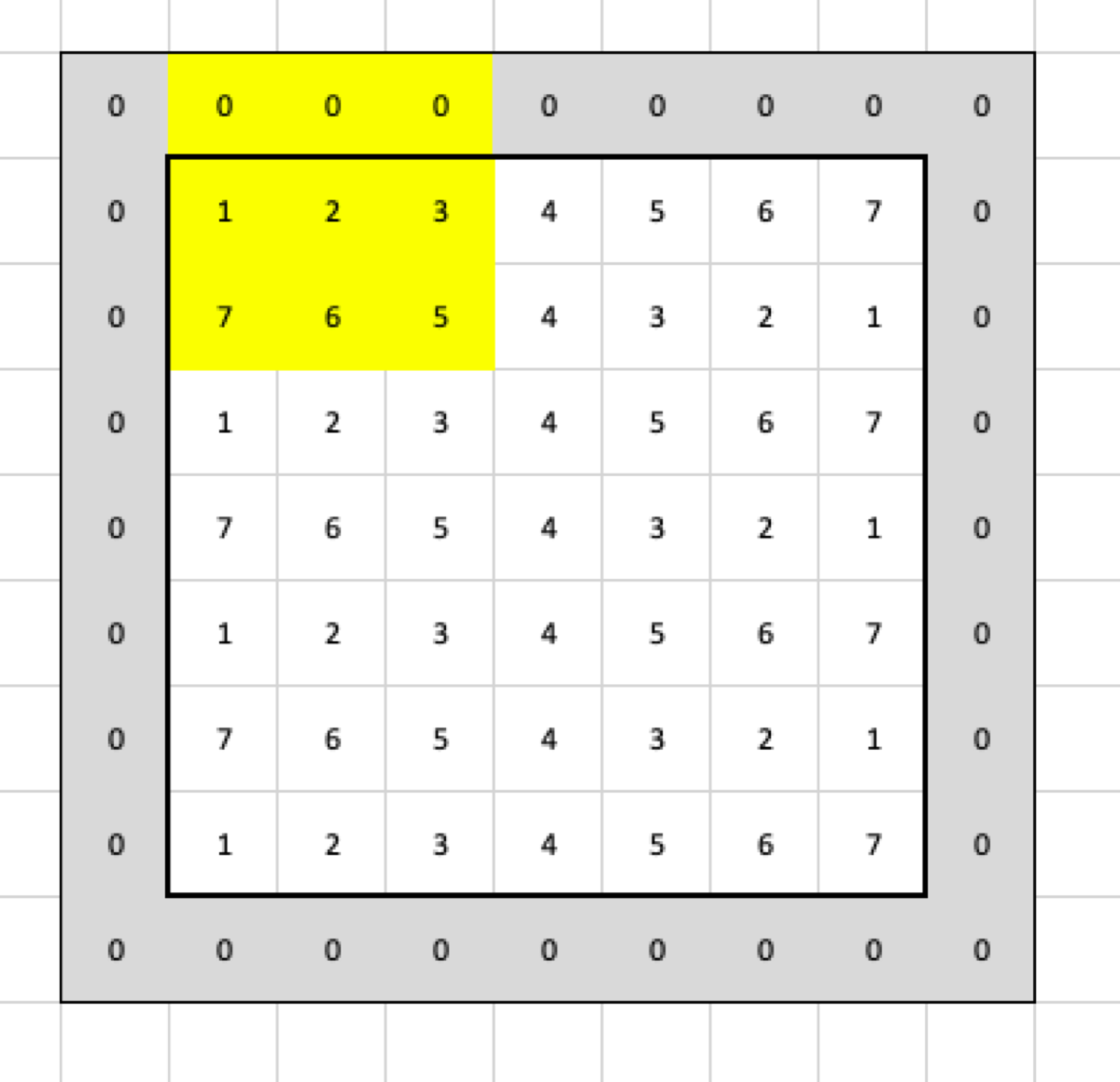
What if I want to have the output in the same size as the input without changing the filter? I must add two columns and two rows to the input. If I use zero-padding with size 2, it will mean that I add two rows and two columns which contain only zeros as the border of the input:
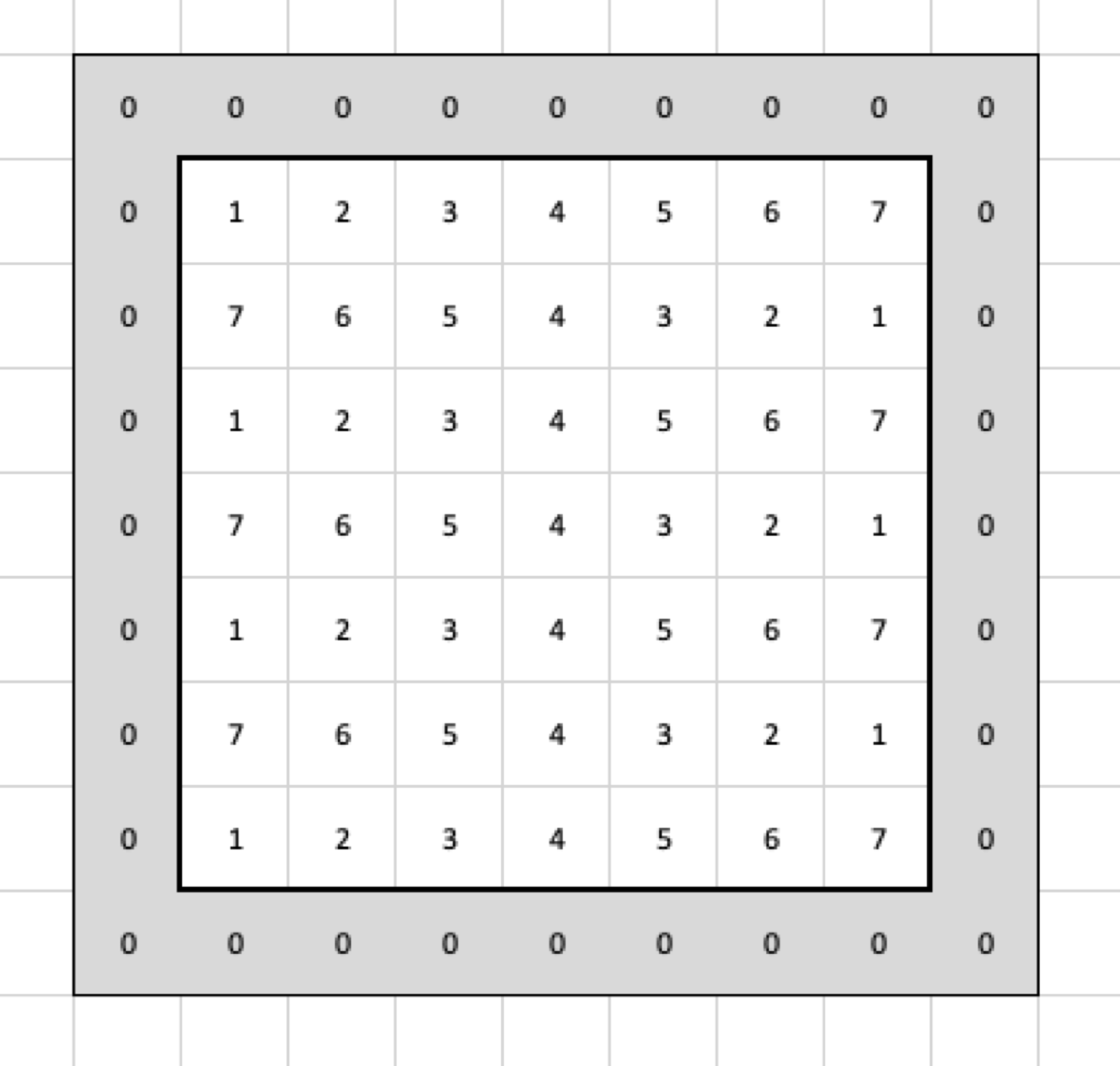
Now, when I apply the filter, it is going to select the following cells:
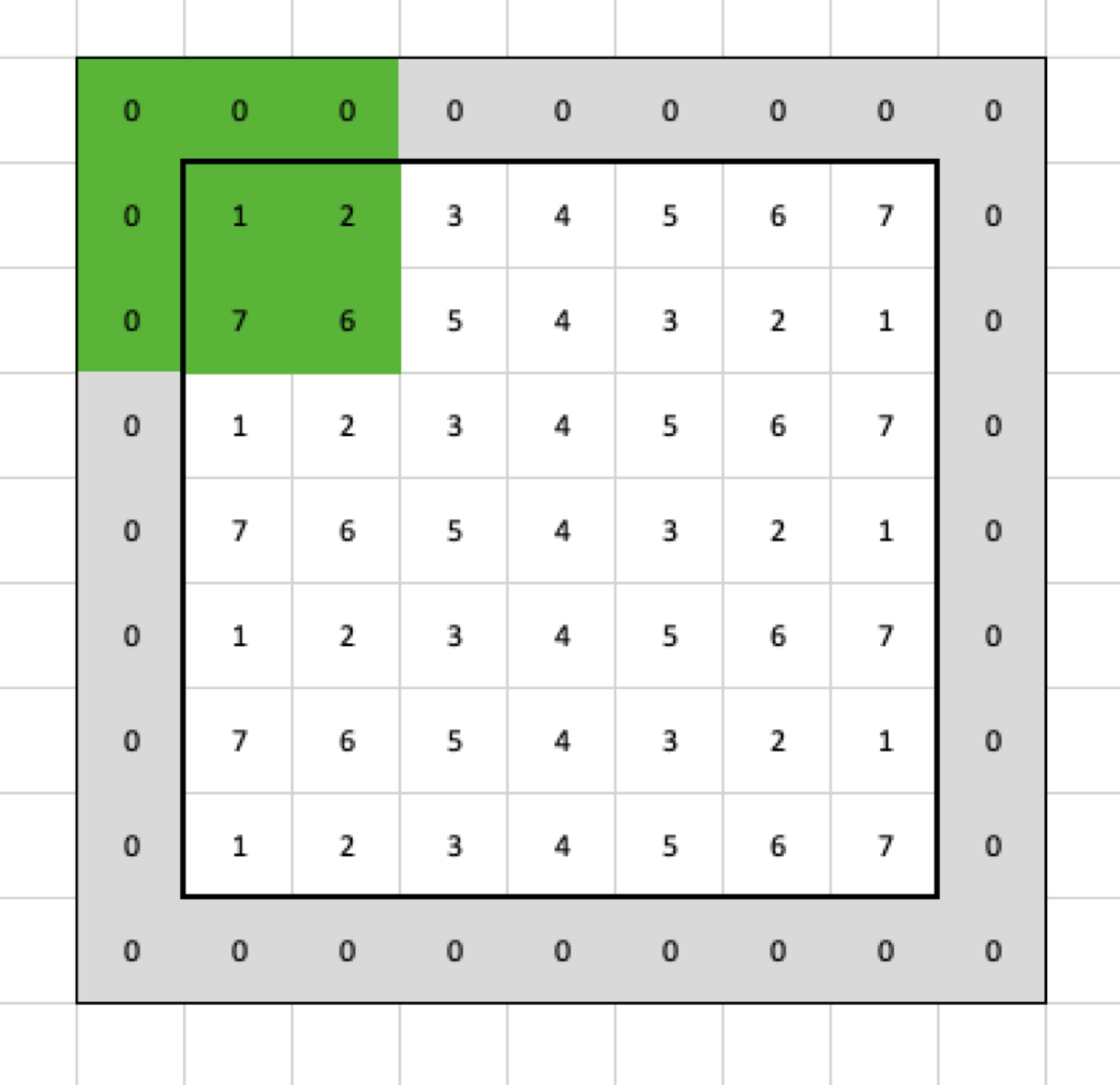
so the max pooling returns this:
In the next step, the filter selects those cells:
and the result looks like this:
When the filter gets applied to all cells, this is going to be the final result:
Stride
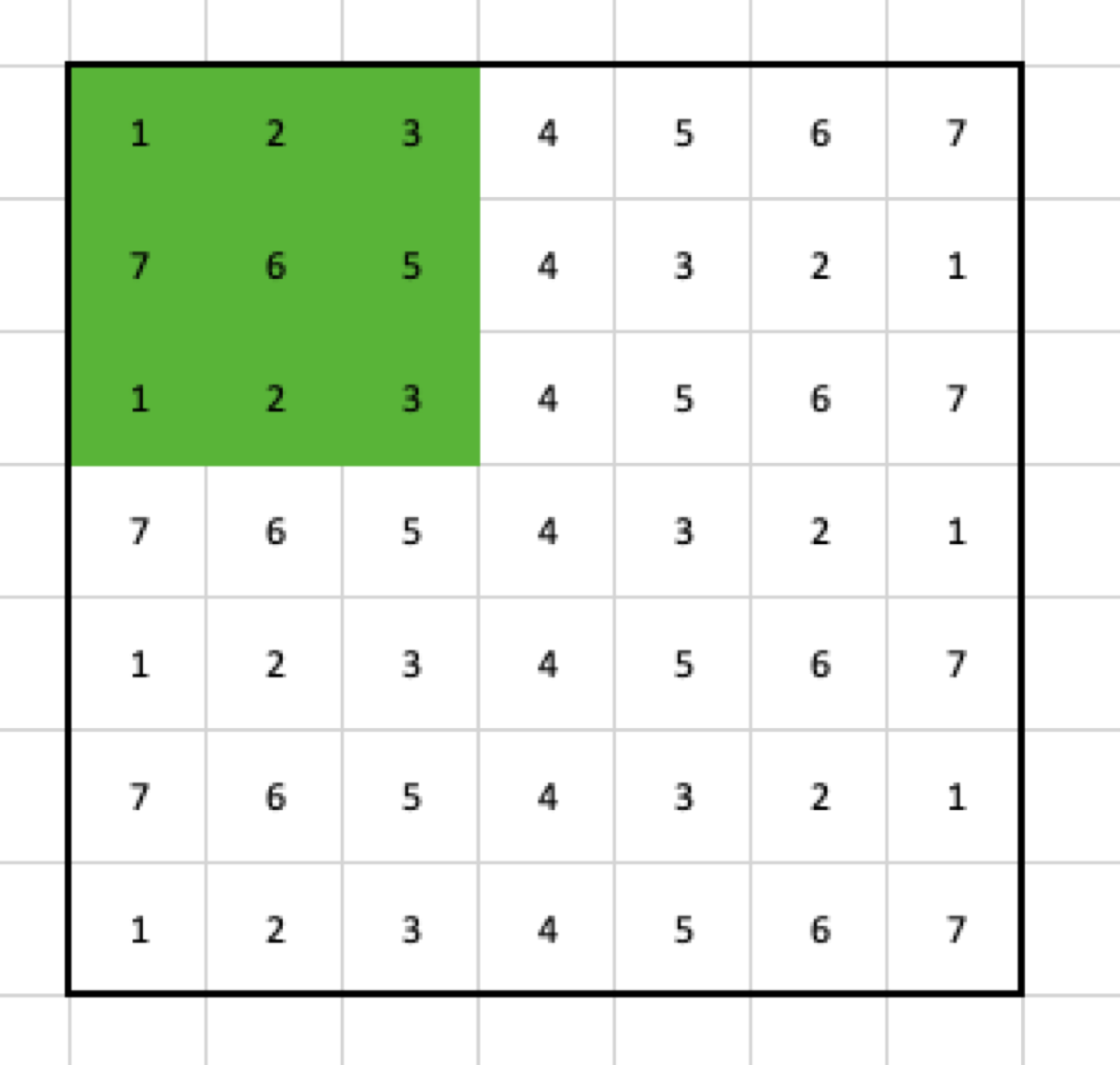
Let’s use the input without padding again, but this time with stride = 2.
In the first step, the filter selects these cells:
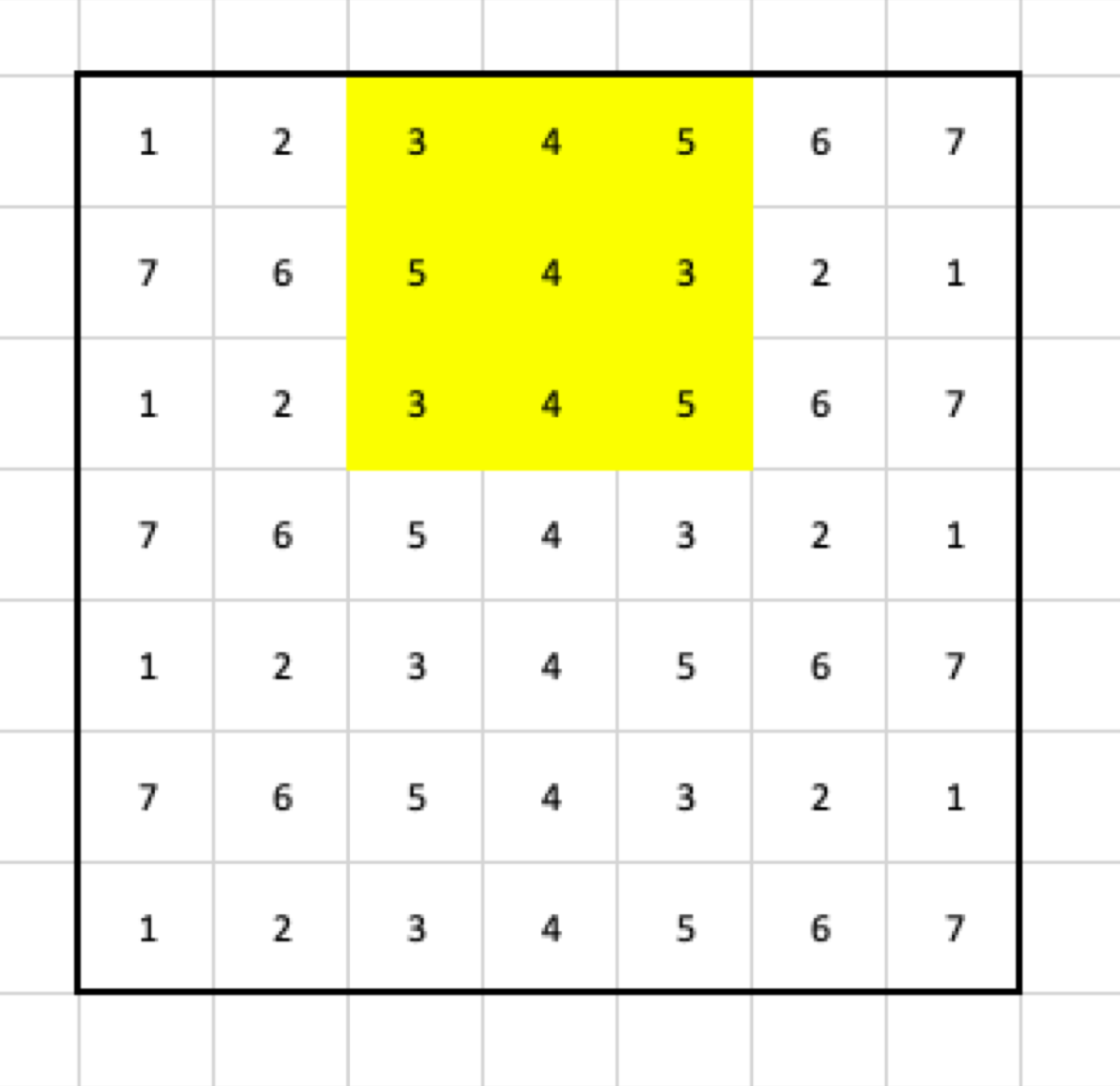
Then, it moves two columns to the right, so the second step selects the following cells:
After those steps, the output contains:
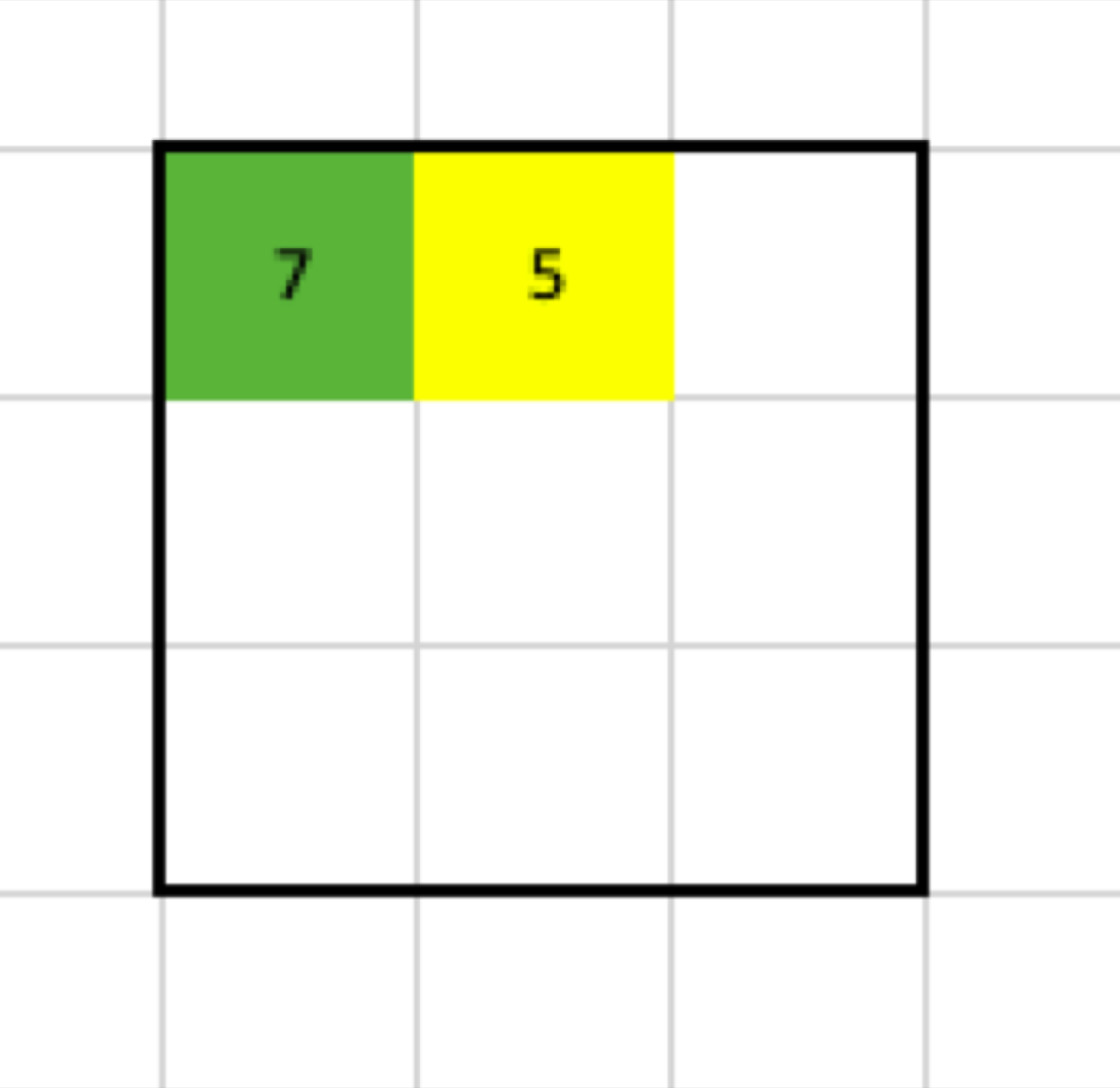
We also see that, when the input is a 7x7 matrix, the filter has size 3x3 with stride 2 and without padding, the output is going to be a 3x3 matrix.
Formula
Things get complicated. Fortunately, there is a formula that lets us calculate the size of the output.
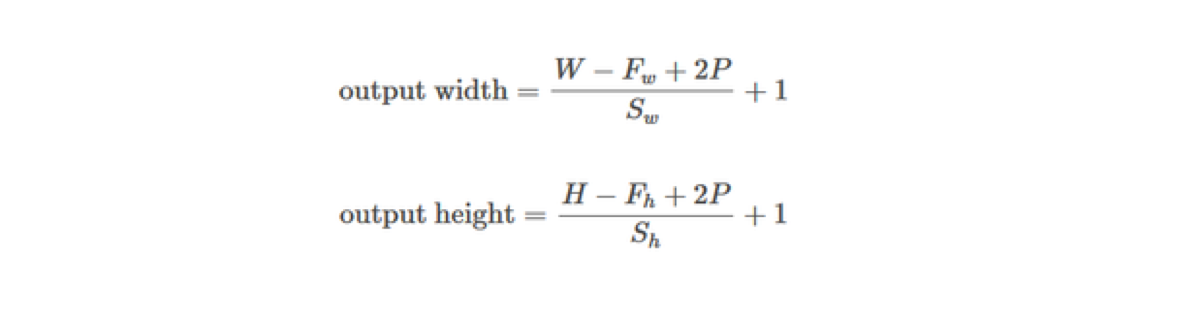
W — the width of the input
F_w — the width of the filter
P — padding
S_w — the horizontal stride
H — the height of the input
F_h — the height of the filter
P — padding
S_h — the vertical stride

