Recently I found a YouTube video from Google about Statistical data sampling. They describe a tool they use to sample production data to get the smallest dataset that covers both all expected cases and all edge cases.

Table of Contents

Goal
Machine learning-based implementation

After sampling the production data, they run some regression/smoke tests with the sample as the input parameters. The goal is to check whether the software works in all the cases which have been observed so far in production.

Obviously, this method does not give us a detailed test report as unit testing. It is also not a replacement of integration tests, but it can be used to check all data combinations that occurred in production. We can not only make sure that the software does not crash, but also measure CPU and memory utilization during the test.

Unfortunately, in the video, they do not say anything useful about the implementation. Google kept it as a secret, but they revealed enough information to help with reproducing the solution.

Their solution is based on statistical data sampling and methods that give us a representative sample of a population.

In my first attempt, I am going to do it differently. Instead of statistical methods, I will use one of the standard machine learning algorithms.

Goal

According to the video, the tool implemented by Google produces a small sample of production data that covers the entire dataset. It also lets the users select the relevant features. Most importantly, their solution is parallelizable with map/reduce.

Machine learning-based implementation

Before I start, I have to generate some fake data which I will use as my “production” dataset.

import pandas as pd
import numpy as np
from scipy.stats import norm

number_of_observations = 10000
RANDOM_STATE = 123

feature1 = norm(loc = 5, scale = 2).rvs(size = number_of_observations, random_state = RANDOM_STATE)
feature2 = norm(loc = 30, scale = 10).rvs(size = number_of_observations, random_state = RANDOM_STATE)
feature3 = norm(loc = 10, scale = 30).rvs(size = number_of_observations, random_state = RANDOM_STATE)

data = pd.DataFrame({
    'feature1': feature1, 'feature2': feature2, 'feature3': feature3
})

Agglomerative clustering

I am going to use the agglomerative clustering algorithm, which works similarly to k-NN. It calculates the distance between samples and puts similar instances in the same cluster.

I decided to use this algorithm because it starts with the number of clusters equal to the number of rows in the dataset, so initially, every observation is in a separate group. After that, the algorithm calculates the distance between groups and merges similar clusters into larger groups.

In the end, I get only two groups (using the default settings) and also a tree of clusters.

from sklearn.cluster import AgglomerativeClustering

clustering = AgglomerativeClustering(compute_full_tree = True)
clustering.fit(data)

from scipy.cluster.hierarchy import fcluster

Because of that, I can defer the decision about the number of samples I need. I will generate the tree of groups and later choose the cut-off point.

When I have the tree of groups, I can decide how many samples I need. From every cluster, I am going to take one sample, so the number of clusters is going to be equal to the number of samples I obtain.

children = clustering.children_

distance = np.arange(children.shape[0])
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.column_stack([children, distance, no_of_observations]).astype(float)
# the code above was taken from: https://github.com/scikit-learn/scikit-learn/blob/70cf4a676caa2d2dad2e3f6e4478d64bcb0506f7/examples/cluster/plot_hierarchical_clustering_dendrogram.py

the_number_of_clusters_i_want = 8
clusters = fcluster(linkage_matrix, the_number_of_clusters_i_want, criterion='maxclust')

data_with_clusters = data
data_with_clusters['cluster'] = pd.Series(clusters)

examples_for_testing = data_with_clusters.groupby('cluster').first()

How many examples do we need?

To decide how many clusters I need, I am going to generate all possible cluster combinations and calculate the maximal distances between generated clusters. The chart shows the maximal distance for groupings with n clusters.

from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

distances = []

for i in range(2, 200):
    the_number_of_clusters_i_want = i
    clusters = fcluster(linkage_matrix, the_number_of_clusters_i_want, criterion='maxclust')

    data_with_clusters = data
    data_with_clusters['cluster'] = pd.Series(clusters)
    grouped = data_with_clusters.groupby('cluster').first()

    distances.append(np.max(cdist(grouped, grouped, 'euclidean')))

plt.plot(range(2, 200), distances)
plt.xlabel('number of clusters')
plt.ylabel('maximal distance')
plt.title('maximal distance per number of clusters')

plt.axvline(np.where(distances == np.max(distances))[0][0] + 1, c = 'red', linestyle = 'dotted')

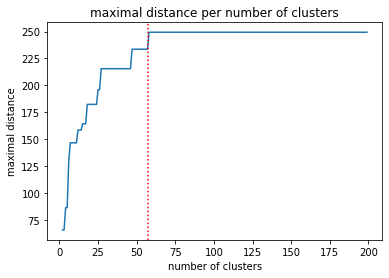
We see that after reaching 57 clusters, the maximal distance stops getting larger. I am going to use that value as my target number of samples.

the_number_of_clusters_i_want = np.where(distances == np.max(distances))[0][0] + 1

clusters = fcluster(linkage_matrix, the_number_of_clusters_i_want, criterion='maxclust')
data_with_clusters = data
data_with_clusters['cluster'] = pd.Series(clusters)

examples_for_testing = data_with_clusters.groupby('cluster').first()
examples_for_testing

Parallelization

That part is going to be relatively easy because I can split the data into shards and apply the hierarchical clustering to every shard separately (this part can be parallelized).

As a result, I am going to get intermediate clusters which contain significantly fewer observations. I can combine those intermediate clusters into one and cluster it again. After this step, I am going to get the final samples set.

Using machine learning for software testing

Goal

Machine learning-based implementation

Agglomerative clustering

How many examples do we need?

Parallelization

How to measure the similarity of sequence values

How to run Airflow in Docker (with a persistent database)

Using machine learning for software testing

Goal

Machine learning-based implementation

Agglomerative clustering

How many examples do we need?

Parallelization

How to measure the similarity of sequence values

How to run Airflow in Docker (with a persistent database)

Related Posts

A.I. in production: your next stylist is going to be a neural network

What is the difference between training, validation, and test sets in machine learning

How to plot the decision trees from XGBoost classifier